Profile

|
Publications
Learning Direction Fields for Quad Mesh Generation

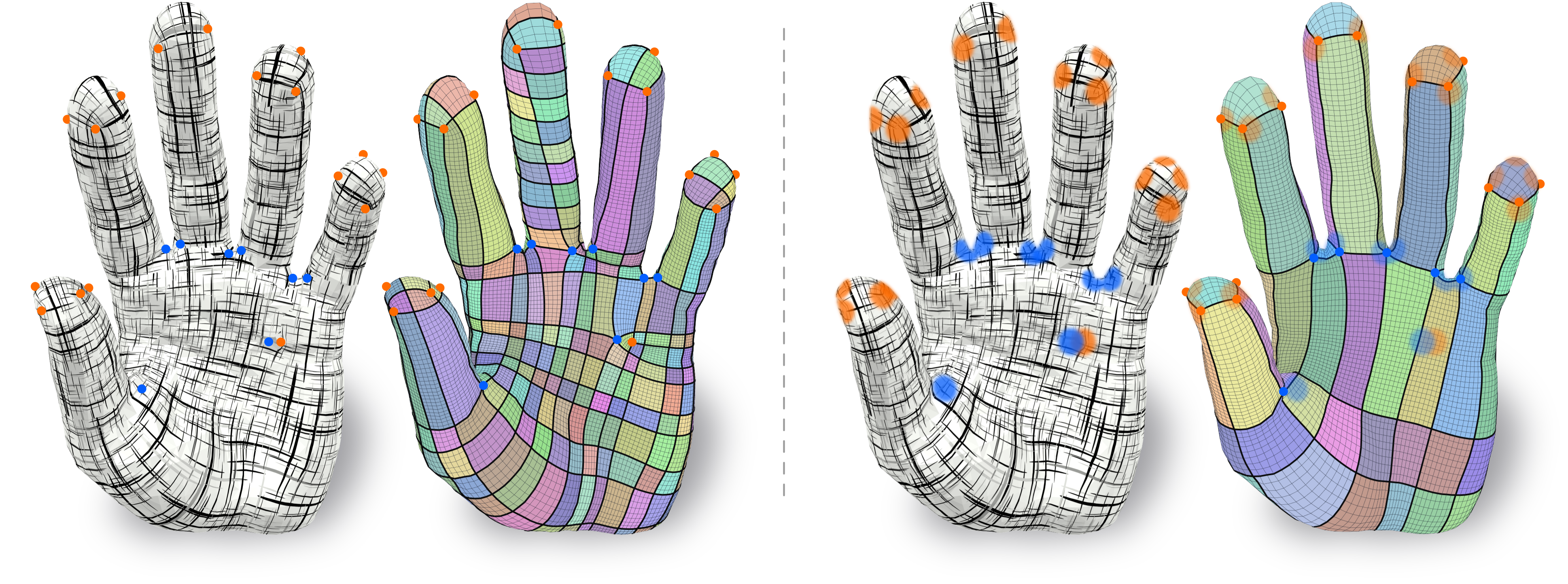
State of the art quadrangulation methods are able to reliably and robustly convert triangle meshes into quad meshes. Most of these methods rely on a dense direction field that is used to align a parametrization from which a quad mesh can be extracted. In this context, the aforementioned direction field is of particular importance, as it plays a key role in determining the structure of the generated quad mesh. If there are no user-provided directions available, the direction field is usually interpolated from a subset of principal curvature directions. To this end, a number of heuristics that aim to identify significant surface regions have been proposed. Unfortunately, the resulting fields often fail to capture the structure found in meshes created by human experts. This is due to the fact that experienced designers can leverage their domain knowledge in order to optimize a mesh for a specific application. In the context of physics simulation, for example, a designer might prefer an alignment and local refinement that facilitates a more accurate numerical simulation. Similarly, a character artist may prefer an alignment that makes the resulting mesh easier to animate. Crucially, this higher level domain knowledge cannot be easily extracted from local curvature information alone. Motivated by this issue, we propose a data-driven approach to the computation of direction fields that allows us to mimic the structure found in existing meshes, which could originate from human experts or other sources. More specifically, we make use of a neural network that aggregates global and local shape information in order to compute a direction field that can be used to guide a parametrization-based quad meshing method. Our approach is a first step towards addressing this challenging problem with a fully automatic learning-based method. We show that compared to classical techniques our data-driven approach combined with a robust model-driven method, is able to produce results that more closely exhibit the ground truth structure of a synthetic dataset (i.e. a manually designed quad mesh template fitted to a variety of human body types in a set of different poses).
@article{dielen2021learning_direction_fields,
title={Learning Direction Fields for Quad Mesh Generation},
author={Dielen, Alexander and Lim, Isaak and Lyon, Max and Kobbelt, Leif},
year={2021},
journal={Computer Graphics Forum},
volume={40},
number={5},
}
Simpler Quad Layouts using Relaxed Singularities
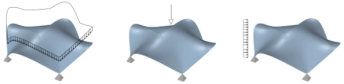
A common approach to automatic quad layout generation on surfaces is to, in a first stage, decide on the positioning of irregular layout vertices, followed by finding sensible layout edges connecting these vertices and partitioning the surface into quadrilateral patches in a second stage. While this two-step approach reduces the problem's complexity, this separation also limits the result quality. In the worst case, the set of layout vertices fixed in the first stage without consideration of the second may not even permit a valid quad layout. We propose an algorithm for the creation of quad layouts in which the initial layout vertices can be adjusted in the second stage. Whenever beneficial for layout quality or even validity, these vertices may be moved within a prescribed radius or even be removed. Our algorithm is based on a robust quantization strategy, turning a continuous T-mesh structure into a discrete layout. We show the effectiveness of our algorithm on a variety of inputs.
» Show BibTeX
@article{lyon2021simplerlayouts,
title={Simpler Quad Layouts using Relaxed Singularities},
author={Lyon, Max and Campen, Marcel and Kobbelt, Leif},
year={2021},
journal={Computer Graphics Forum},
volume={40},
number={5},
}
Quad Layouts via Constrained T-Mesh Quantization

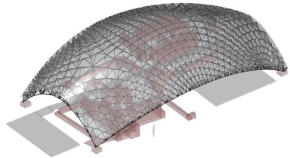
We present a robust and fast method for the creation of conforming quad layouts on surfaces. Our algorithm is based on the quantization of a T-mesh, i.e. an assignment of integer lengths to the sides of a non-conforming rectangular partition of the surface. This representation has the benefit of being able to encode an infinite number of layout connectivity options in a finite manner, which guarantees that a valid layout can always be found. We carefully construct the T-mesh from a given seamless parametrization such that the algorithm can provide guarantees on the results' quality. In particular, the user can specify a bound on the angular deviation of layout edges from prescribed directions. We solve an integer linear program (ILP) to find a coarse quad layout adhering to that maximal deviation. Our algorithm is guaranteed to yield a conforming quad layout free of T-junctions together with bounded angle distortion. Our results show that the presented method is fast, reliable, and achieves high quality layouts.
» Show BibTeX
@article{Lyon:2021:Quad,
title = {Quad Layouts via Constrained T-Mesh Quantization},
author = {Lyon, Max and Campen, Marcel and Kobbelt, Leif},
journal = {Computer Graphics Forum},
volume = {40},
number = {2},
year = {2021}
}
Cost Minimizing Local Anisotropic Quad Mesh Refinement

Quad meshes as a surface representation have many conceptual advantages over triangle meshes. Their edges can naturally be aligned to principal curvatures of the underlying surface and they have the flexibility to create strongly anisotropic cells without causing excessively small inner angles. While in recent years a lot of progress has been made towards generating high quality uniform quad meshes for arbitrary shapes, their adaptive and anisotropic refinement remains difficult since a single edge split might propagate across the entire surface in order to maintain consistency. In this paper we present a novel refinement technique which finds the optimal trade-off between number of resulting elements and inserted singularities according to a user prescribed weighting. Our algorithm takes as input a quad mesh with those edges tagged that are prescribed to be refined. It then formulates a binary optimization problem that minimizes the number of additional edges which need to be split in order to maintain consistency. Valence 3 and 5 singularities have to be introduced in the transition region between refined and unrefined regions of the mesh. The optimization hence computes the optimal trade-off and places singularities strategically in order to minimize the number of consistency splits — or avoids singularities where this causes only a small number of additional splits. When applying the refinement scheme iteratively, we extend our binary optimization formulation such that previous splits can be undone if this prevents degenerate cells with small inner angles that otherwise might occur in anisotropic regions or in the vicinity of singularities. We demonstrate on a number of challenging examples that the algorithm performs well in practice.
» Show BibTeX
@article{Lyon:2020:Cost,
title = {Cost Minimizing Local Anisotropic Quad Mesh Refinement},
author = {Lyon, Max and Bommes, David and Kobbelt, Leif},
journal = {Computer Graphics Forum},
volume = {39},
number = {5},
year = {2020},
doi = {10.1111/cgf.14076}
}
Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing

The generation of quad meshes based on surface parametrization techniques has proven to be a versatile approach. These techniques quantize an initial seamless parametrization so as to obtain an integer grid map implying a pure quad mesh. State-of-the-art methods following this approach have to assume that the surface to be meshed either has no boundary, or has a boundary which the resulting mesh is supposed to be aligned to. In a variety of applications this is not desirable and non-boundary-aligned meshes or grid-parametrizations are preferred. We thus present a technique to robustly generate integer grid maps which are either boundary-aligned, non-boundary-aligned, or partially boundary-aligned, just as required by different applications. We thereby generalize previous work to this broader setting. This enables the reliable generation of trimmed quad meshes with partial elements along the boundary, preferable in various scenarios, from tiled texturing over design and modeling to fabrication and architecture, due to fewer constraints and hence higher overall mesh quality and other benefits in terms of aesthetics and flexibility.
@article{Lyon:2019:TrimmedQuadMeshing,
author = "Lyon, Max and Campen, Marcel and Bommes, David and Kobbelt, Leif",
title = "Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing",
journal = "ACM Transactions on Graphics",
volume = 38,
number = 4,
year = 2019
}
Form Finding of Stress Adapted Folding as a Lightweight Structure Under Different Load Cases
In steel construction, the use of folds is limited to longitudinal folds (e.g. trapezoidal sheets). The efficiency of creases can be increased by aligning the folding pattern to the principal stresses or to their directions. This paper presents a form-finding approach to use the material as homogeneously as possible. In addition to the purely geometric alignment according to the stress directions, it also allows the stress intensity to be taken into account during form-finding. A trajectory mesh of the principle stresses is generated on the basis of which the structure is derived. The relationships between the stress lines distance, progression and stress intensity are discussed and implemented in the approaches of form-finding. Building on this, this paper additionally deals with the question of which load case is the most effective basis for designing the crease pattern when several load cases can act simultaneously.
@article {Musto:2019:2518-6582:1,
title = "Form finding of stress adapted folding as a lightweight structure under different load cases",
journal = "Proceedings of IASS Annual Symposia",
parent_itemid = "infobike://iass/piass",
publishercode ="iass",
year = "2019",
volume = "2019",
number = "13",
publication date ="2019-10-07T00:00:00",
pages = "1-8",
itemtype = "ARTICLE",
issn = "2518-6582",
eissn = "2518-6582",
url = "https://www.ingentaconnect.com/content/iass/piass/2019/00002019/00000013/art00006",
keyword = "lightweight-construction, folding, Mixed-Integer Quadrangulation, principle stress lines",
author = "Musto, Juan and Lyon, Max and Trautz, Martin and Kobbelt, Leif",
abstract = "In steel construction, the use of folds is limited to longitudinal folds (e.g. trapezoidal sheets). The efficiency of creases can be increased by aligning the folding pattern to the principal stresses or to their directions. This paper presents a form-finding approach to use the material
as homogeneously as possible. In addition to the purely geometric alignment according to the stress directions, it also allows the stress intensity to be taken into account during form-finding. A trajectory mesh of the principle stresses is generated on the basis of which the structure is
derived. The relationships between the stress lines distance, progression and stress intensity are discussed and implemented in the approaches of form-finding. Building on this, this paper additionally deals with the question of which load case is the most effective basis for designing
the crease pattern when several load cases can act simultaneously.",
}
Beanspruchungsoptimierte Faltungen aus Stahl für selbsttragende Raumfaltwerke
Der Einsatz von Faltungen beschränkt sich im Bauwesen auf Longitudinalfaltungen (Trapezbleche) und regelmäßige Faltungen. Raumfaltwerke und Faltleichtbauplatten, räumlich gekrümmte und dreidimensionale Flächentragwerke sind Desiderate eines Leichtbaus mit Stahlblechen. Raumfaltwerke bestehen vorwiegend aus regelmäßigen Faltmuster, die auf Tesselierung mit Primitivflächen (Drei-und Vierecke) basieren. Um die Effizienz dieser Leichtbaustrukturen zu verbessern, liegt es nahe, statt regelmäßige und auf geometrischen Prinzipien basierende Faltmuster umzusetzen, Faltmuster nach Maßgabe nach Maßgabe der der Beanspruchungen bzw. der Beanspruchungsverteilung anzuwenden. Hierzu ist ein Formfindungsprozess zu entwickeln, der auf der Generierung eines Trajektoriennetzes basiert, das aus dem maßgeblichen Lastfall (formgebenden Lastfall) abgeleitet wird. Der Vergleich des Masseneinsatzes und der Traglast der Faltungen, die auf geometrischer Basis erzeugt wurden mit einer auf Basis des Trajektoriennetzes entwickelten Faltung zeigt die Veränderung der Effizienz .
@article{https://doi.org/10.1002/bate.201900024,
author = {Musto, Juan and Lyon, Max and Trautz, Martin and Kobbelt, Leif},
title = {Beanspruchungsoptimierte Faltungen aus Stahl für selbsttragende Raumfaltwerke},
journal = {Bautechnik},
volume = {96},
number = {12},
pages = {902-911},
keywords = {Leichtbau, Faltungen, Hauptspannungstrajektorien, Mixed-Integer Quadrangulation, lightweight-construction, folgings, principle stress trajectories, mixed-integer quadrangulation, Stahlbau, Leichtbau, Steel construction, lightweight construction},
doi = {https://doi.org/10.1002/bate.201900024},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1002/bate.201900024},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1002/bate.201900024},
abstract = {Abstract Der Einsatz von Faltungen beschränkt sich im Bauwesen auf Longitudinalfaltungen (Trapezbleche) und regelmäßige Faltungen. Raumfaltwerke und Faltleichtbauplatten, räumlich gekrümmte und dreidimensionale Flächentragwerke sind Desiderate eines Leichtbaus mit Stahlblechen. Raumfaltwerke bestehen vorwiegend aus regelmäßigen Faltmustern, die auf Tesselierung mit Primitivflächen (Drei- und Vierecke) basieren. Um die Effizienz dieser Leichtbaustrukturen zu verbessern, liegt es nahe, statt regelmäßige und auf geometrischen Prinzipien basierende Faltmuster umzusetzen, Faltmuster nach Maßgabe der Beanspruchungen bzw. der Beanspruchungsverteilung anzuwenden. Hierzu ist ein Formfindungsprozess zu entwickeln, der auf der Generierung eines Trajektoriennetzes basiert, das aus dem maßgeblichen Lastfall (formgebenden Lastfall) abgeleitet wird. Der Vergleich des Masseneinsatzes und der Traglast der Faltungen, die auf geometrischer Basis erzeugt wurden, mit einer auf Basis des Trajektoriennetzes entwickelten Faltung zeigt die Veränderung der Effizienz.},
year = {2019}
}
Selective Padding for Polycube-based Hexahedral Meshing
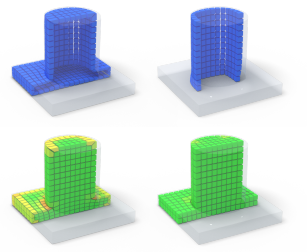
Abstract Hexahedral meshes generated from polycube mapping often exhibit a low number of singularities but also poor-quality elements located near the surface. It is thus necessary to improve the overall mesh quality, in terms of the minimum scaled Jacobian (MSJ) or average SJ (ASJ). Improving the quality may be obtained via global padding (or pillowing), which pushes the singularities inside by adding an extra layer of hexahedra on the entire domain boundary. Such a global padding operation suffers from a large increase of complexity, with unnecessary hexahedra added. In addition, the quality of elements near the boundary may decrease. We propose a novel optimization method which inserts sheets of hexahedra so as to perform selective padding, where it is most needed for improving the mesh quality. A sheet can pad part of the domain boundary, traverse the domain and form singularities. Our global formulation, based on solving a binary problem, enables us to control the balance between quality improvement, increase of complexity and number of singularities. We show in a series of experiments that our approach increases the MSJ value and preserves (or even improves) the ASJ, while adding fewer hexahedra than global padding.
@article{Cherchi2018SelectivePadding,
author = {Cherchi, G. and Alliez, P. and Scateni, R. and Lyon, M. and Bommes, D.},
title = {Selective Padding for Polycube-Based Hexahedral Meshing},
journal = {Computer Graphics Forum},
volume = {38},
number = {1},
pages = {580-591},
keywords = {computational geometry, modelling, physically based modelling, mesh generation, I.3.5 Computer Graphics: Computational Geometry and Object Modeling—Curve, surface, solid, and object representations},
doi = {https://doi.org/10.1111/cgf.13593},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.13593},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.13593},
abstract = {Abstract Hexahedral meshes generated from polycube mapping often exhibit a low number of singularities but also poor-quality elements located near the surface. It is thus necessary to improve the overall mesh quality, in terms of the minimum scaled Jacobian (MSJ) or average SJ (ASJ). Improving the quality may be obtained via global padding (or pillowing), which pushes the singularities inside by adding an extra layer of hexahedra on the entire domain boundary. Such a global padding operation suffers from a large increase of complexity, with unnecessary hexahedra added. In addition, the quality of elements near the boundary may decrease. We propose a novel optimization method which inserts sheets of hexahedra so as to perform selective padding, where it is most needed for improving the mesh quality. A sheet can pad part of the domain boundary, traverse the domain and form singularities. Our global formulation, based on solving a binary problem, enables us to control the balance between quality improvement, increase of complexity and number of singularities. We show in a series of experiments that our approach increases the MSJ value and preserves (or even improves) the ASJ, while adding fewer hexahedra than global padding.},
year = {2019}
}
HexEx: Robust Hexahedral Mesh Extraction

State-of-the-art hex meshing algorithms consist of three steps: Frame-field design, parametrization generation, and mesh extraction. However, while the first two steps are usually discussed in detail, the last step is often not well studied. In this paper, we fully concentrate on reliable mesh extraction.
Parametrization methods employ computationally expensive countermeasures to avoid mapping input tetrahedra to degenerate or flipped tetrahedra in the parameter domain because such a parametrization does not define a proper hexahedral mesh. Nevertheless, there is no known technique that can guarantee the complete absence of such artifacts.
We tackle this problem from the other side by developing a mesh extraction algorithm which is extremely robust against typical imperfections in the parametrization. First, a sanitization process cleans up numerical inconsistencies of the parameter values caused by limited precision solvers and floating-point number representation. On the sanitized parametrization, we extract vertices and so-called darts based on intersections of the integer grid with the parametric image of the tetrahedral mesh. The darts are reliably interconnected by tracing within the parametrization and thus define the topology of the hexahedral mesh. In a postprocessing step, we let certain pairs of darts cancel each other, counteracting the effect of flipped regions of the parametrization. With this strategy, our algorithm is able to robustly extract hexahedral meshes from imperfect parametrizations which previously would have been considered defective. The algorithm will be published as an open source library.
@article{Lyon:2016:HexEx,
author = "Lyon, Max and Bommes, David and Kobbelt, Leif",
title = "HexEx: Robust Hexahedral Mesh Extraction",
journal = "ACM Transactions on Graphics",
volume = 35,
number = 4,
year = 2016
}

