 |
OpenMesh
|
 |
OpenMesh
|
This section describes the underlying data structure that is used to store the mesh entities (items) vertices, edges, faces, and their connectivity information.
There are many popular data structures used to represent polygonal meshes. For a detailed comparison of them refer to the papers at the end of this section.
The data structure used in this project is the so called halfedge data structure . While face-based structures store their connectivity in faces referencing their vertices and neighbors, edge-based structures put the connectivity information into the edges. Each edge references its two vertices, the faces it belongs to and the two next edges in these faces. If one now splits the edges (i.e. an edge connecting vertex A and vertex B becomes two directed halfeges from A to B and vice versa) one gets a halfedge-based data structure. The following figure illustrates the way connectivity is stored in this structure:
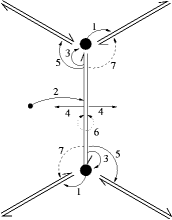
|
|
Having these links between the items, it is now possible to circulate around a face in order to enumerate all its vertices, halgedges, or neighboring faces. When starting at a vertex' halfedge and iterating to the opposite of its previous one, one can easily circulate around this vertex and get all its one-ring neighbors, the incoming/outgoing halfedges, or the adjacent faces. All this functionality is encapsulated into the so-called circulators , described in Mesh Iterators and Circulators.
While one does not need to store the previous halfedge (7) explicitly, because it can be derived from the links to the next halfedges, one may do so for the sake of performance. In fact, the previous halfedge is stored by default (OpenMesh::DefaultTraits). Using traits and attributes the previous halfedge can removed, to gain memory. This kind of mesh customization is explained in Specifying your MyMesh.
While the halfedge-based structures usually consume more memory than their face-based counter-parts they have the following important advantages:
if-then branchings, the halfedge structure provides this funcionality without conditional branching in constant time.References
S. Campagna, L. Kobbelt, H.-P. Seidel, Directed Edges - A Scalable Representation For Triangle Meshes , ACM Journal of Graphics Tools 3 (4), 1998.
Lutz Kettner, Using Generic Programming for Designing a Data Structure for Polyhedral Surfaces, in Proc. 14th Annual ACM Symp. on Computational Geometry, 1998.