Linear Analysis of Nonlinear Constraints for Interactive Geometric Modeling
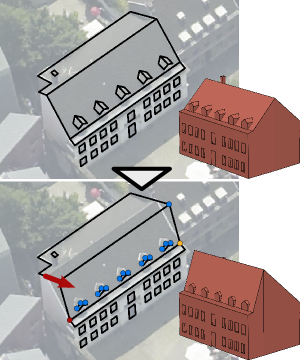
Thanks to its flexibility and power to handle even complex geometric relations, 3D geometric modeling with nonlinear constraints is an attractive extension of traditional shape editing approaches. However, existing approaches to analyze and solve constraint systems usually fail to meet the two main challenges of an interactive 3D modeling system: For each atomic editing operation, it is crucial to adjust as few auxiliary vertices as possible in order to not destroy the user's earlier editing effort. Furthermore, the whole constraint resolution pipeline is required to run in real-time to enable a fluent, interactive workflow. To address both issues, we propose a novel constraint analysis and solution scheme based on a key observation: While the computation of actual vertex positions requires nonlinear techniques, under few simplifying assumptions the determination of the minimal set of to-be-updated vertices can be performed on a linearization of the constraint functions. Posing the constraint analysis phase as the solution of an under-determined linear system with as few non-zero elements as possible enables us to exploit an efficient strategy for the Cardinality Minimization problem known from the field of Compressed Sensing, resulting in an algorithm capable of handling hundreds of vertices and constraints in real-time. We demonstrate at the example of an image-based modeling system for architectural models that this approach performs very well in practical applications.
Awards:

