Bijective Maps from Simplicial Foliations

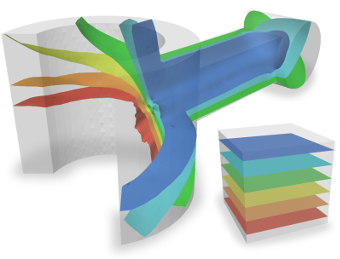
This paper presents a method for bijective parametrization of 2D and 3D objects over canonical domains. While a range of solutions for the two-dimensional case are well-known, our method guarantees bijectivity of mappings also for a large, combinatorially-defined class of tetrahedral meshes (shellable meshes). The key concept in our method is the piecewise-linear (PL) foliation, decomposing the mesh into one-dimensional submanifolds and reducing the mapping problem to parametrization of a lower-dimensional manifold (a foliation section). The maps resulting from these foliations are proved to be bijective and continuous, and shown to have provably bijective PL approximations. We describe exact, numerically robust evaluation methods and demonstrate our implementation's capabilities on a large variety of meshes.