Layout Embedding via Combinatorial Optimization

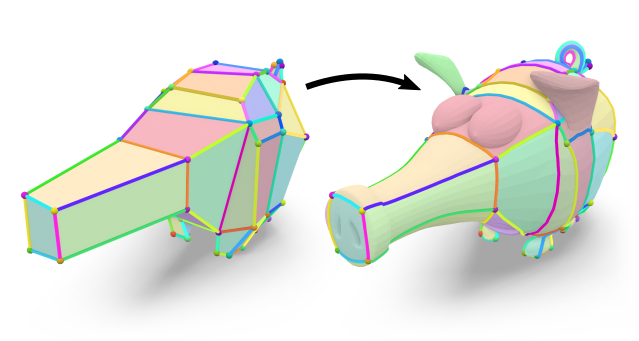
We consider the problem of injectively embedding a given graph connectivity (a layout) into a target surface. Starting from prescribed positions of layout vertices, the task is to embed all layout edges as intersection-free paths on the surface. Besides merely geometric choices (the shape of paths) this problem is especially challenging due to its topological degrees of freedom (how to route paths around layout vertices). The problem is typically addressed through a sequence of shortest path insertions, ordered by a greedy heuristic. Such insertion sequences are not guaranteed to be optimal: Early path insertions can potentially force later paths into unexpected homotopy classes. We show how common greedy methods can easily produce embeddings of dramatically bad quality, rendering such methods unsuitable for automatic processing pipelines. Instead, we strive to find the optimal order of insertions, i.e. the one that minimizes the total path length of the embedding. We demonstrate that, despite the vast combinatorial solution space, this problem can be effectively solved on simply-connected domains via a custom-tailored branch-and-bound strategy. This enables directly using the resulting embeddings in downstream applications which cannot recover from initializations in a wrong homotopy class. We demonstrate the robustness of our method on a shape dataset by embedding a common template layout per category, and show applications in quad meshing and inter-surface mapping.

• Honorable mention for Günter Enderle Best Paper Award
• Graphics Replicability Stamp