Spectral Quadrangulation with Orientation and Alignment Control

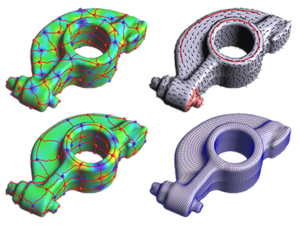
This paper presents a new quadrangulation algorithm, extending the spectral surface quadrangulation approach where the coarse quadrangular structure is derived from the Morse-Smale complex of an eigenfunction of the Laplacian operator on the input mesh. In contrast to the original scheme, we provide flexible explicit controls of the shape, size, orientation and feature alignment of the quadrangular faces. We achieve this by proper selection of the optimal eigenvalue (shape), by adaption of the area term in the Laplacian operator (size), and by adding special constraints to the Laplace eigenproblem (orientation and alignment). By solving a generalized eigenproblem we can generate a scalar field on the mesh whose Morse-Smale complex is of high quality and satisfies all the user requirements. The final quadrilateral mesh is generated from the Morse- Smale complex by computing a globally smooth parametrization. Here we additionally introduce edge constraints to preserve user specified feature lines accurately.