A Robust Two-Step Procedure for Quad-Dominant Remeshing
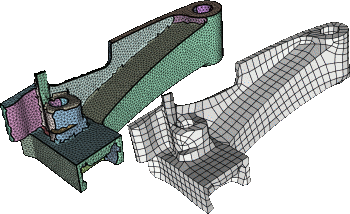
We propose a new technique for quad-dominant remeshing which separates the local regularity requirements from the global alignment requirements by working in two steps. In the first step, we apply a slight variant of variational shape approximation in order to segment the input mesh into patches which capture the global structure of the processed object. Then we compute an optimized quad-mesh for every patch by generating a finite set of candidate curves and applying a combinatorial optimization procedure. Since the optimization is performed independently for each patch, we can afford more complex operations while keeping the overall computation times at a reasonable level. Our quad-meshing technique is robust even for noisy meshes and meshes with isotropic or flat regions since it does not rely on the generation of curves by integration along estimated principal curvature directions. Instead we compute a conformal parametrization for each patch and generate the quad-mesh from curves with minimum bending energy in the 2D parameter domain. Mesh consistency between patches is guaranteed by simply using the same set of sample points along the common boundary curve. The resulting quad-meshes are of high-quality locally (shape of the quads) as well as globally (global alignment) which allows us to even generate fairly coarse quad-meshes that can be used as Catmull-Clark control meshes.

