Welcome







The research and teaching activities at our institute focus on geometry acquisition and processing, on interactive visualization, and on related areas such as computer vision, photo-realistic image synthesis, and ultra high speed multimedia data transmission.
In our projects we are cooperating with various industry companies as well as with academic research groups around the world. Results are published and presented at high-profile conferences and symposia. Additional funding sources, among others, are the Deutsche Forschungsgemeinschaft and the European Union.
News
| • |
We have a paper on greedily generating artwork using Bézier segments at VMV 2023. |
May 23, 2023 |
| • |
Our paper on surface maps received the Günter Enderle Best Paper Award at Eurographics 2023. |
May 12, 2023 |
| • |
We have a paper on the interactive segmentation of textured point clouds at VMV 2022. |
Oct. 4, 2022 |
| • |
Our paper on automatic differentiation received the best paper award (1st place) at the Symposium on Geometry Processing 2022 |
July 6, 2022 |
| • |
We have a paper on fast and exact mesh Booleans at SIGGRAPH 2022. |
June 13, 2022 |
| • |
In collaboration with CNIC Madrid we have a paper on the geometry of heart development in Nature Cardiovascular Research. |
May 18, 2022 |
Recent Publications
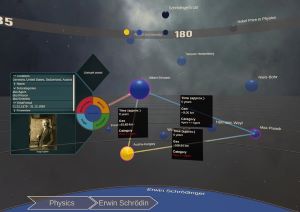 Who Did What When? Discovering Complex Historical Interrelations in Immersive Virtual Reality Konferenz: 2023 IEEE International Symposium on Mixed and Augmented Reality Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments (e.g., persons or events). In this paper, we present a novel interactive exploration tool for historical data in VR, which represents fragments as spheres in a 3D environment and arranges them around the user based on their temporal, geo, categorical and semantic similarity. Quantitative and qualitative results from a user study with 29 participants revealed that most participants considered the virtual space and the abstract fragment representation well-suited to explore historical data and to discover complex interrelationships. These results were particularly underlined by high usability scores in terms of attractiveness, stimulation, and novelty, while researching historical facts with our system did not impose unexpectedly high task loads. Additionally, the insights from our post-study interviews provided valuable suggestions for future developments to further expand the possibilities of our system. 
|
 Greedy Image Approximation for Artwork Generation via Contiguous Bézier Segments 28th International Symposium on Vision, Modeling, and Visualization (VMV) 2023 The automatic creation of digital art has a long history in computer graphics. In this work, we focus on approximating input images to mimic artwork by the artist Kumi Yamashita, as well as the popular scribble art style. Both have in common that the artists create the works by using a single, contiguous thread (Yamashita) or stroke (scribble) that is placed seemingly at random when viewed at close range, but perceived as a tone-mapped picture when viewed from a distance. Our approach takes a rasterized image as input and creates a single, connected path by iteratively sampling a set of candidate segments that extend the current path and greedily selecting the best one. The candidates are sampled according to art style specific constraints, i.e. conforming to continuity constraints in the mathematical sense for the scribble art style. To model the perceptual discrepancy between close and far viewing distances, we minimize the difference between the input image and the image created by rasterizing our path after applying the contrast sensitivity function, which models how human vision blurs images when viewed from a distance. Our approach generalizes to colored images by using one path per color. We evaluate our approach on a wide range of input images and show that it is able to achieve good results for both art styles in grayscale and color. 
|

