Publications
Neural Implicit Shape Editing Using Boundary Sensitivity

Neural fields are receiving increased attention as a geometric representation due to their ability to compactly store detailed and smooth shapes and easily undergo topological changes. Compared to classic geometry representations, however, neural representations do not allow the user to exert intuitive control over the shape. Motivated by this, we leverage boundary sensitivity to express how perturbations in parameters move the shape boundary. This allows to interpret the effect of each learnable parameter and study achievable deformations. With this, we perform geometric editing: finding a parameter update that best approximates a globally prescribed deformation. Prescribing the deformation only locally allows the rest of the shape to change according to some prior, such as semantics or deformation rigidity. Our method is agnostic to the model its training and updates the NN in-place. Furthermore, we show how boundary sensitivity helps to optimize and constrain objectives (such as surface area and volume), which are difficult to compute without first converting to another representation, such as a mesh.
@misc{berzins2023neural,
title={Neural Implicit Shape Editing using Boundary Sensitivity},
author={Arturs Berzins and Moritz Ibing and Leif Kobbelt},
year={2023},
eprint={2304.12951},
archivePrefix={arXiv},
primaryClass={cs.CV}
}
Surface Maps via Adaptive Triangulations

We present a new method to compute continuous and bijective maps (surface homeomorphisms) between two or more genus-0 triangle meshes. In contrast to previous approaches, we decouple the resolution at which a map is represented from the resolution of the input meshes. We discretize maps via common triangulations that approximate the input meshes while remaining in bijective correspondence to them. Both the geometry and the connectivity of these triangulations are optimized with respect to a single objective function that simultaneously controls mapping distortion, triangulation quality, and approximation error. A discrete-continuous optimization algorithm performs both energy-based remeshing as well as global second-order optimization of vertex positions, parametrized via the sphere. With this, we combine the disciplines of compatible remeshing and surface map optimization in a unified formulation and make a contribution in both fields. While existing compatible remeshing algorithms often operate on a fixed pre-computed surface map, we can now globally update this correspondence during remeshing. On the other hand, bijective surface-to-surface map optimization previously required computing costly overlay meshes that are inherently tied to the input mesh resolution. We achieve significant complexity reduction by instead assessing distortion between the approximating triangulations. This new map representation is inherently more robust than previous overlay-based approaches, is less intricate to implement, and naturally supports mapping between more than two surfaces. Moreover, it enables adaptive multi-resolution schemes that, e.g., first align corresponding surface regions at coarse resolutions before refining the map where needed. We demonstrate significant speedups and increased flexibility over state-of-the art mapping algorithms at similar map quality, and also provide a reference implementation of the method.
» Show BibTeX
@article{schmidt2023surface,
title={Surface Maps via Adaptive Triangulations},
author={Schmidt, Patrick and Pieper, D\"orte and Kobbelt, Leif},
year={2023},
journal={Computer Graphics Forum},
volume={42},
number={2},
}
Who Did What When? Discovering Complex Historical Interrelations in Immersive Virtual Reality
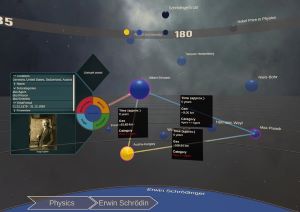
Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments (e.g., persons or events). In this paper, we present a novel interactive exploration tool for historical data in VR, which represents fragments as spheres in a 3D environment and arranges them around the user based on their temporal, geo, categorical and semantic similarity. Quantitative and qualitative results from a user study with 29 participants revealed that most participants considered the virtual space and the abstract fragment representation well-suited to explore historical data and to discover complex interrelationships. These results were particularly underlined by high usability scores in terms of attractiveness, stimulation, and novelty, while researching historical facts with our system did not impose unexpectedly high task loads. Additionally, the insights from our post-study interviews provided valuable suggestions for future developments to further expand the possibilities of our system.
@INPROCEEDINGS{10316480,
author={Derksen, Melanie and Becker, Julia and Elahi, Mohammad Fazleh and Maier, Angelika and Maile, Marius and Pätzold, Ingo and Penningroth, Jonas and Reglin, Bettina and Rothgänger, Markus and Cimiano, Philipp and Schubert, Erich and Schwandt, Silke and Kuhlen, Torsten and Botsch, Mario and Weissker, Tim},
booktitle={2023 IEEE International Symposium on Mixed and Augmented Reality (ISMAR)},
title={{Who Did What When? Discovering Complex Historical Interrelations in Immersive Virtual Reality}},
year={2023},
volume={},
number={},
pages={129-137},
doi={10.1109/ISMAR59233.2023.00027}}
Towards Discovering Meaningful Historical Relationships in Virtual Reality

Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments. We are working on a novel interactive exploration tool for historical data in virtual reality, which arranges fragments in a 3D environment based on their temporal, spatial and categorical proximity to a reference fragment. In this poster, we report on an initial expert review of our approach, giving us valuable insights into the use cases and requirements that inform our further developments.
@INPROCEEDINGS{Derksen2023,
author={Derksen, Melanie and Weissker, Tim and Kuhlen, Torsten and Botsch, Mario},
booktitle={2023 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW)},
title={Towards Discovering Meaningful Historical Relationships in Virtual Reality},
year={2023},
volume={},
number={},
pages={697-698},
doi={10.1109/VRW58643.2023.00191}}
Octree Transformer: Autoregressive 3D Shape Generation on Hierarchically Structured Sequences
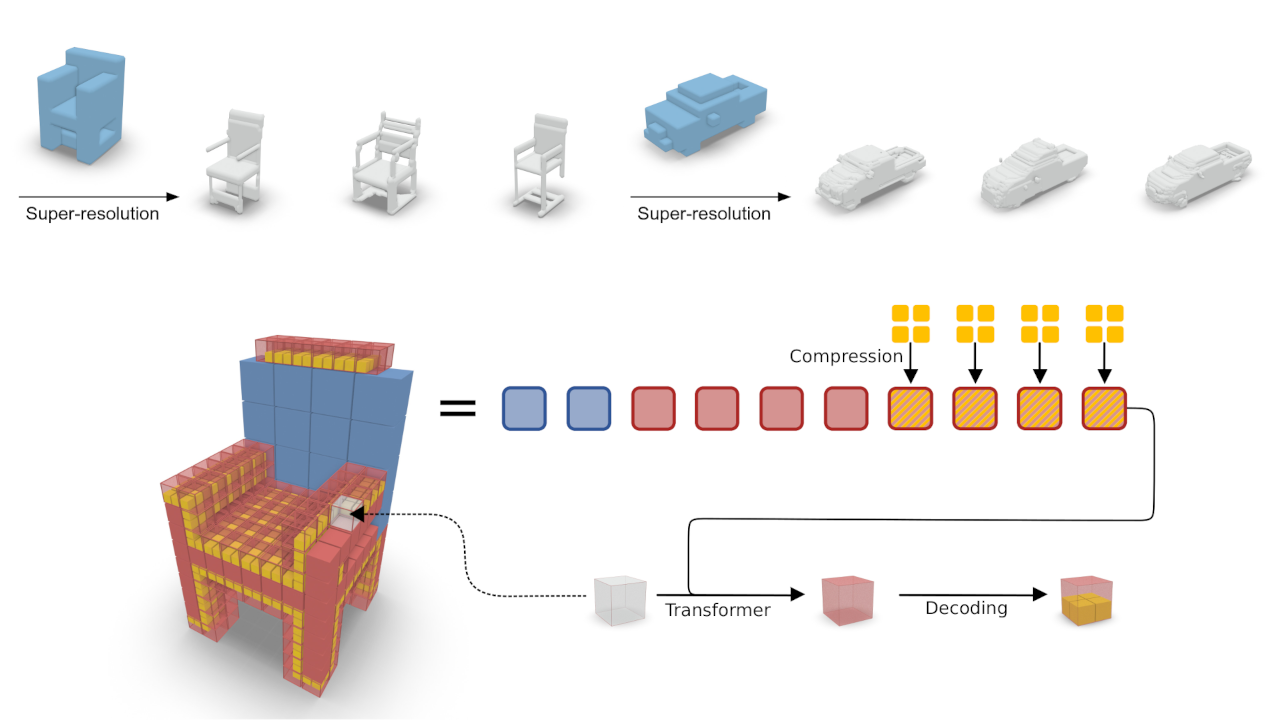
Autoregressive models have proven to be very powerful in NLP text generation tasks and lately have gained pop ularity for image generation as well. However, they have seen limited use for the synthesis of 3D shapes so far. This is mainly due to the lack of a straightforward way to linearize 3D data as well as to scaling problems with the length of the resulting sequences when describing complex shapes. In this work we address both of these problems. We use octrees as a compact hierarchical shape representation that can be sequentialized by traversal ordering. Moreover, we introduce an adaptive compression scheme, that significantly reduces sequence lengths and thus enables their effective generation with a transformer, while still allowing fully autoregressive sampling and parallel training. We demonstrate the performance of our model by performing superresolution and comparing against the state-of-the-art in shape generation.
@inproceedings{ibing_octree,
author = {Moritz Ibing and
Gregor Kobsik and
Leif Kobbelt},
title = {Octree Transformer: Autoregressive 3D Shape Generation on Hierarchically Structured Sequences},
booktitle = {{IEEE/CVF} Conference on Computer Vision and Pattern Recognition Workshops,
{CVPR} Workshops 2023},
publisher = {{IEEE}},
year = {2023},
}
Localized Latent Updates for Fine-Tuning Vision-Language Models
Although massive pre-trained vision-language models like CLIP show impressive generalization capabilities for many tasks, still it often remains necessary to fine-tune them for improved performance on specific datasets. When doing so, it is desirable that updating the model is fast and that the model does not lose its capabilities on data outside of the dataset, as is often the case with classical fine-tuning approaches. In this work we suggest a lightweight adapter that only updates the models predictions close to seen datapoints. We demonstrate the effectiveness and speed of this relatively simple approach in the context of few-shot learning, where our results both on classes seen and unseen during training are comparable with or improve on the state of the art.
@inproceedings{ibing_localized,
author = {Moritz Ibing and
Isaak Lim and
Leif Kobbelt},
title = {Localized Latent Updates for Fine-Tuning Vision-Language Models},
booktitle = {{IEEE/CVF} Conference on Computer Vision and Pattern Recognition Workshops,
{CVPR} Workshops 2023},
publisher = {{IEEE}},
year = {2023},
}
Greedy Image Approximation for Artwork Generation via Contiguous Bézier Segments

The automatic creation of digital art has a long history in computer graphics. In this work, we focus on approximating input images to mimic artwork by the artist Kumi Yamashita, as well as the popular scribble art style. Both have in common that the artists create the works by using a single, contiguous thread (Yamashita) or stroke (scribble) that is placed seemingly at random when viewed at close range, but perceived as a tone-mapped picture when viewed from a distance. Our approach takes a rasterized image as input and creates a single, connected path by iteratively sampling a set of candidate segments that extend the current path and greedily selecting the best one. The candidates are sampled according to art style specific constraints, i.e. conforming to continuity constraints in the mathematical sense for the scribble art style. To model the perceptual discrepancy between close and far viewing distances, we minimize the difference between the input image and the image created by rasterizing our path after applying the contrast sensitivity function, which models how human vision blurs images when viewed from a distance. Our approach generalizes to colored images by using one path per color. We evaluate our approach on a wide range of input images and show that it is able to achieve good results for both art styles in grayscale and color.
@inproceedings{nehringwirxel2023greedy,
title={Greedy Image Approximation for Artwork Generation via Contiguous B{\'{e}}zier Segments},
author={Nehring-Wirxel, Julius and Lim, Isaak and Kobbelt, Leif},
booktitle={28th International Symposium on Vision, Modeling, and Visualization, VMV 2023},
year={2023}
}
Previous Year (2022)

