Profile

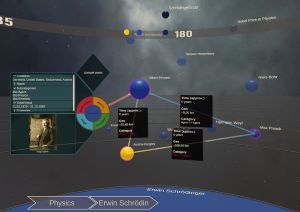
Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments (e.g., persons or events). In this paper, we present a novel interactive exploration tool for historical data in VR, which represents fragments as spheres in a 3D environment and arranges them around the user based on their temporal, geo, categorical and semantic similarity. Quantitative and qualitative results from a user study with 29 participants revealed that most participants considered the virtual space and the abstract fragment representation well-suited to explore historical data and to discover complex interrelationships. These results were particularly underlined by high usability scores in terms of attractiveness, stimulation, and novelty, while researching historical facts with our system did not impose unexpectedly high task loads. Additionally, the insights from our post-study interviews provided valuable suggestions for future developments to further expand the possibilities of our system.

Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments. We are working on a novel interactive exploration tool for historical data in virtual reality, which arranges fragments in a 3D environment based on their temporal, spatial and categorical proximity to a reference fragment. In this poster, we report on an initial expert review of our approach, giving us valuable insights into the use cases and requirements that inform our further developments.

In the last years triangle meshes have become increasingly popular and are nowadays intensively used in many different areas of computer graphics and geometry processing. In classical CAGD irregular triangle meshes developed into a valuable alternative to traditional spline surfaces, since their conceptual simplicity allows for more flexible and highly efficient processing. Moreover, the consequent use of triangle meshes as surface representation avoids error-prone conversions, e.g., from CAD surfaces to mesh-based input data of numerical simulations. Besides classical geometric modeling, other major areas frequently employing triangle meshes are computer games and movie production. In this context geometric models are often acquired by 3D scanning techniques and have to undergo post-processing and shape optimization techniques before being actually used in production.

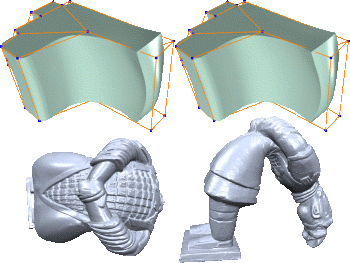
Multiresolution shape editing performs global deformations while preserving fine surface details by modifying a smooth base surface and reconstructing the modified detailed surface as a normal displacement from it. Since two non-trivial operators (deformation and reconstruction) are involved, the computational complexity can become too high for real-time deformations of complex models. We present an efficient technique for evaluating multiresolution deformations of high-resolution triangle meshes directly on the GPU. By precomputing the deformation functions as well as their gradient information we can map both the deformation and the reconstruction operator to the GPU, which enables us to reconstruct the deformed positions and sufficiently close approximations of the normal vectors in the vertex shader in a single rendering pass. This allows us to render dynamically deforming 3D models several times faster than on the CPU. We demonstrate the application of our technique to two modern multiresolution approaches: one based on (irregular) displaced subdivision surfaces and the other one on volumetric space deformation using radial basis functions.

We present a new method for 3D shape modeling that achieves intuitive and robust deformations by emulating physically plausible surface behavior inspired by thin shells and plates. The surface mesh is embedded in a layer of volumetric prisms, which are coupled through non-linear, elastic forces. To deform the mesh, prisms are rigidly transformed to satisfy user constraints while minimizing the elastic energy. The rigidity of the prisms prevents degenerations even under extreme deformations, making the method numerically stable. For the underlying geometric optimization we employ both local and global shape matching techniques. Our modeling framework allows for the specification of various geometrically intuitive parameters that provide control over the physical surface behavior. While computationally more involved than previous methods, our approach significantly improves robustness and simplifies user interaction for large, complex deformations.

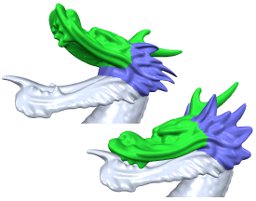
Current surface-based methods for interactive freeform editing of high resolution 3D models are very powerful, but at the same time require a certain minimum tessellation or sampling quality in order to guarantee sufficient robustness. In contrast to this, space deformation techniques do not depend on the underlying surface representation and hence are affected neither by its complexity nor by its quality aspects. However, while analogously to surface-based methods high quality deformations can be derived from variational optimization, the major drawback lies in the computation and evaluation, which is considerably more expensive for volumetric space deformations. In this paper we present techniques which allow us to use triharmonic radial basis functions for real-time freeform shape editing. An incremental least-squares method enables us to approximately solve the involved linear systems in a robust and efficient manner and by precomputing a special set of deformation basis functions we are able to significantly reduce the per-frame costs. Moreover, evaluating these linear basis functions on the GPU finally allows us to deform highly complex polygon meshes or point-based models at a rate of 30M vertices or 13M splats per second, respectively.

Because of their conceptual simplicity and superior flexibility, point-based geometries evolved into a valuable alternative to surface representations based on polygonal meshes. Elliptical surface splats were shown to allow for high-quality anti-aliased rendering by sophisticated EWA filtering. Since the publication of the original software-based EWA splatting, several authors tried to map this technique to the GPU in order to exploit hardware acceleration. Due to the lacking support for splat primitives, these methods always have to find a trade-off between rendering quality and rendering performance. In this paper, we discuss the capabilities of today's GPUs for hardware-accelerated surface splatting. We present an approach that achieves a quality comparable to the original EWA splatting at a rate of more than 20M elliptical splats per second. In contrast to previous GPU renderers, our method provides per-pixel Phong shading even for dynamically changing geometries and high-quality anti-aliasing by employing a screen-space pre-filter in addition to the object-space reconstruction filter. The use of deferred shading techniques effectively avoids unnecessary shader computations and additionally provides a clear separation between the rasterization and the shading of elliptical splats, which considerably simplifies the development of custom shaders. We demonstrate quality, efficiency, and flexibility of our approach by showing several shaders on a range of models.

Mario Botsch, David Bommes, Leif Kobbelt

The use of polygonal mesh representations for freeform geometry enables the formulation of many important geometry processing tasks as the solution of one or several linear systems. As a consequence, the key ingredient for efficient algorithms is a fast procedure to solve linear systems. A large class of standard problems can further be shown to lead more specifically to sparse, symmetric, and positive definite systems, that allow for a numerically robust and efficient solution. In this paper we discuss and evaluate the use of \emph{sparse direct solvers} for such kind of systems in geometry processing applications, since in our experiments they turned out to be superior even to highly optimized multigrid methods, but at the same time were considerably easier to use and implement. Although the methods we present are well known in the field of high performance computing, we observed that they are in practice surprisingly rarely applied to geometry processing problems.

We present a freeform modeling framework for unstructured triangle meshes which is based on constraint shape optimization. The goal is to simplify the user interaction even for quite complex freeform or multiresolution modifications. The user first sets various boundary constraints to define a custom tailored (abstract) basis function which is adjusted to a given design task. The actual modification is then controlled by moving one single 9-dof manipulator object. The technique can handle arbitrary support regions and piecewise boundary conditions with smoothness ranging continuously from C0 to C2. To more naturally adapt the modification to the shape of the support region, the deformed surface can be tuned to bend with anisotropic stiffness. We are able to achieve real-time response in an interactive design session even for complex meshes by precomputing a set of scalar-valued basis functions that correspond to the degrees of freedom of the manipulator by which the user controls the modification.

Providing a thorough mathematical foundation, multiresolution modeling is the standard approach for global surface deformations that preserve fine surface details in an intuitive and plausible manner. A given shape is decomposed into a smooth low-frequency base surface and high-frequency detail information. Adding these details back onto a deformed version of the base surface results in the desired modification. Using a suitable detail encoding, the connectivity of the base surface is not restricted to be the same as that of the original surface. We propose to exploit this degree of freedom to improve both robustness and efficiency of multiresolution shape editing. In several approaches the modified base surface is computed by solving a linear system of discretized Laplacians. By remeshing the base surface such that the Voronoi areas of its vertices are equalized, we turn the unsymmetric surface-related linear system into a symmetric one, such that simpler, more robust, and more efficient solvers can be applied. The high regularity of the remeshed base surface further removes numerical problems caused by mesh degeneracies and results in a better discretization of the Laplacian operator. The remeshing is performed on the low-frequency base surface only, while the connectivity of the original surface is kept fixed. Hence, this functionality can be encapsulated inside a multiresolution kernel and is thus completely hidden from the user.

Surface splatting has developed into a valuable alternative to triangle meshes when it comes to rendering of highly detailed massive datasets. However, even highly accurate splat approximations of the given geometry may sometimes not provide a sufficient rendering quality since surface lighting mostly depends on normal vectors whose deviation is not bounded by the Hausdorff approximation error. Moreover, current point-based rendering systems usually associate a constant normal vector with each splat, leading to rendering results which are comparable to flat or Gouraud shading for polygon meshes. In contrast, we propose to base the lighting of a splat on a linearly varying normal field associated with it, and we show that the resulting Phong Splats provide a visual quality which is far superior to existing approaches. We present a simple and effective way to construct a Phong splat representation for a given set of input samples. Our surface splatting system is implemented completely based on vertex and pixel shaders of current GPUs and achieves a splat rate of up to 4M Phong shaded, filtered, and blended splats per second. In contrast to previous work, our scan conversion is projectively correct per pixel, leading to more accurate visualization and clipping at sharp features.

We present a novel algorithm for accurate, high quality point rendering, which is based on the formulation of the splatting process using homogeneous coordinates. In contrast to previous methods, this leads to perspective correct splat shapes, avoiding artifacts such as holes due to the approximation of the perspective projection. Further, our algorithm implements the EWA resampling filter, hence providing high image quality with anisotropic texture filtering. We also present an extension of our rendering primitive that allows the display of sharp edges and corners. Finally, we describe an efficient implementation of the algorithm based on vertex and fragment programs of current GPUs.

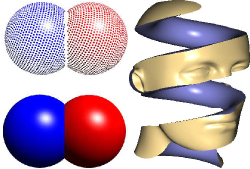
In recent years point-based geometry has gained increasing attention as an alternative surface representation, both for efficient rendering and for flexible geometry processing of highly complex 3D-models. Point sampled objects do neither have to store nor to maintain globally consistent topological information. Therefore they are more flexible compared to triangle meshes when it comes to handling highly complex or dynamically changing shapes. In this paper, we make an attempt to give an overview of the various point-based methods that have been proposed over the last years. In particular we review and evaluate different shape representations, geometric algorithms, and rendering methods which use points as a universal graphics primitive.

In an increasing number of applications triangle meshes represent a flexible and efficient alternative to traditional NURBS-based surface representations. Especially in engineering applications it is crucial to guarantee that a prescribed approximation tolerance to a given reference geometry is respected for any combination of geometric algorithms that are applied when processing a triangle mesh. We propose a simple and generic method for computing the distance of a given polygonal mesh to the reference surface, based on a linear approximation of its signed distance field. Exploiting the hardware acceleration of modern GPUs allows us to perform up to 3M triangle checks per second, enabling real-time distance evaluations even for complex geometries. An additional feature of our approach is the accurate high-quality distance visualization of dynamically changing meshes at a rate of 15M triangles per second. Due to its generality, the presented approach can be used to enhance any mesh processing method by global error control, guaranteeing the resulting mesh to stay within a prescribed error tolerance. The application examples that we present include mesh decimation, mesh smoothing and freeform mesh deformation.

We propose a new representation for multiresolution models which uses volume elements enclosed between the different resolution levels to encode the detail information. Keeping these displacement volumes locally constant during a deformation of the base surface leads to a natural behaviour of the detail features. The corresponding reconstruction operator can be implemented efficiently by a hierarchical iterative relaxation scheme, providing close to interactive response times for moderately complex models. Based on this representation we implement a multiresolution editing tool for irregular polygon meshes that allows the designer to freely edit the base surface of a multiresolution model without having to care about self-intersections in the respective detailed surface. We demonstrate the effectiveness and robustness of the reconstruction by several examples with real-world data.

In the last years point-based rendering has been shown to offer the potential to outperform traditional triangle based rendering both in speed and visual quality when it comes to processing highly complex models. Existing surface splatting techniques achieve superior visual quality by proper filtering but they are still limited in rendering speed. On the other hand the increasing availability and programmability of graphics hardware lead to the developement of very efficient hardware-accelerated rendering methods. However, since no filtered splats are used, these approaches trade visual quality for rendering speed. In this paper we propose a rendering framework for point-based geometry providing high visual quality as well as efficient rendering. Our approach is based on a two-pass splatting technique with Gaussian filtering, resulting in a visual quality comparable to existing software rendering systems. Using programmable graphics hardware we delegate all expensive rendering tasks to the GPU, thereby minimizing data transfer and saving CPU resources. The proposed system renders up to 28M mid-quality or up to 10M high-quality surface splats per second on the latest graphics hardware.

The most important concepts for the handling and storage of freeform shapes in geometry processing applications are parametric representations and volumetric representations. Both have their specific advantages and drawbacks. While the algebraic complexity of volumetric representations S = {(x, y, z) | f (x, y, z) = 0} is independent from the shape complexity, the domain OMEGA of a parametric representation f : OMEGA to S usually has to have the same structure as the surface S itself (which sometimes makes it necessary to update the domain when the surface is modified). On the other hand, the topology of a parametrically defined surface can be controlled explicitly while in a volumetric representation, the surface topology can change accidentally during deformation. A volumetric representation reduces distance queries or inside/outside tests to mere function evaluations but the geodesic neighborhood relation between surface points is difficult to resolve. As a consequence, it seems promising to combine parametric and volumetric representations to effectively exploit both advantages.
In this talk, a number of applications is presented and discussed where such a combination leads to efficient and numerically stable algorithms for the solution of various geometry processing tasks. These applications include surface remeshing, mesh fairing, global error control for mesh decimation and smoothing, and topology control for levelset surfaces.

We propose a highly efficient hierarchical representation for point sampled geometry that automatically balances sampling density and point coordinate quantization. The representation is very compact with a memory consumption of far less than 2 bits per point position which does not depend on the quantization precision. We present an efficient rendering algorithm that exploits the hierarchical structure of the representation to perform fast 3D transformations and shading. The algorithm is extended to surface splatting which yields high quality anti-aliased and water tight surface renderings. Our pure software implementation renders up to 14 million Phong shaded and textured samples per second and about 4 million anti-aliased surface splats on a commodity PC. This is more than a factor 10 times faster than previous algorithms.

We describe the implementation of a half-edge data structure for the static representation and dynamic handling of arbitrary polygonal meshes. The particular design of the data structures and classes aims at maximum flexibility and high performance. We achieve this by using generative programming concepts which allow the compiler to resolve most of the special case handling decisions at compile time. We evaluate our data structure based on prototypic implementations of mesh processing applications such as decimation and smoothing.

The representation of geometric objects based on volumetric data structures has advantages in many geometry processing applications that require, e.g., fast surface interrogation or boolean operations such as intersection and union. However, surface based algorithms like shape optimization (fairing) or freeform modeling often need a topological manifold representation where neighborhood information within the surface is explicitly available. Consequently, it is necessary to find effective conversion algorithms to generate explicit surface descriptions for the geometry which is implicitly defined by a volumetric data set. Since volume data is usually sampled on a regular grid with a given step width, we often observe severe alias artifacts at sharp features on the extracted surfaces. In this paper we present a new technique for surface extraction that performs feature sensitive sampling and thus reduces these alias effects while keeping the simple algorithmic structure of the standard Marching Cubes algorithm. We demonstrate the effectiveness of the new technique with a number of application examples ranging from CSG modeling and simulation to surface reconstruction and remeshing of polygonal models.

Efficient surface reconstruction and reverse engineering techniques are usually based on a polygonal mesh representation of the geometry: the resulting models emerge from piecewise linear interpolation of a set of sample points. The quality of the reconstruction not only depends on the number and density of the sample points but also on their alignment to sharp and rounded features of the original geometry. Bad alignment can lead to severe alias artifacts. In this paper we present a sampling pattern for feature and blend regions which minimizes these alias errors. We show how to improve the quality of a given polygonal mesh model by resampling its feature and blend regions within an interactive framework. We further demonstrate sophisticated modeling operations that can be implemented based on this resampling technique.

When using triangle meshes in numerical simulations or other sophisticated downstream applications, we have to guarantee that no degenerate faces are present since they have, e.g., no well defined normal vectors. In this paper we present a simple but effective algorithm to remove such artifacts from a given triangle mesh. The central problem is to make this algorithm numerically robust because degenerate triangles are usually the source for all kinds of numerical instabilities. Our algorithm is based on a slicing technique that cuts a set of planes through the given polygonal model. The mesh slicing operator only uses numerically stable predicates and therefore is able to split faces in a controlled manner. In combination with a custom tailored mesh decimation scheme we are able to remove the degenerate faces from meshes like those typically generated by tesselation units in CAD systems.

While traditional computer aided design (CAD) is mainly based on piecewise polynomial surface representations, the recent advances in the efficient handling of polygonal meshes have made available a set of powerful techniques which enable sophisticated modeling operations on freeform shapes. In this tutorial we are going to give a detailed introduction into the various techniques that have been proposed over the last years. Those techniques address important issues such as surface generation from discrete samples (e.g. laser scans) or from control meshes (ab initio design); complexity control by adjusting the level of detail of a given 3D-model to the current application or to the available hardware resources; advanced mesh optimization techniques that are based on the numerical simulation of physical material (e.g. membranes or thin plates) and finally the generation and modification of hierarchical representations which enable sophisticated multiresolution modeling functionality. We present an interactive system for the generation of high quality triangle meshes that allows us to handle hybrid geometry (point clouds, polygons,...) as input data. In order to be able to robustly process huge data sets, we exploit graphics hardware features like the raster manager and the z-buffer for specific sub-tasks in the overall procedure. By this we significantly accelerate the stitching of mesh patches and obtain an algorithm for sub-sampling the data points in linear time. The target resolution and the triangle alignment in sub-regions of the resulting mesh can be controlled by adjusting the screen resolution and viewing transformation. An intuitive user interface provides a flexible tool for application dependent optimization of the mesh.

We present an interactive system for the generation of high quality triangle meshes that allows us to handle hybrid geometry (point clouds, polygons,...) as input data. In order to be able to robustly process huge data sets, we exploit graphics hardware features like the raster manager and the z-buffer for specific sub-tasks in the overall procedure. By this we significantly accelerate the stitching of mesh patches and obtain an algorithm for sub-sampling the data points in linear time. The target resolution and the triangle alignment in sub-regions of the resulting mesh can be controlled by adjusting the screen resolution and viewing transformation. An intuitive user interface provides a flexible tool for application dependent optimization of the mesh.

We present a technique for remeshing irregular triangles meshes where the distribution and alignment can be adapted to the underlying geometry. Following the interactive virtual range scanner approach we overcome aliasing problems by introducing a special sampling technique. A sampling grid that can be aligned to the local features of the mesh is constructed interactively in an intuitive way and without adding reasonable overhead to the virtual scanning process.