Profile

Most classical constructions of low-discrepancy point sets are based on generalizations of the one-dimensional binary van der Corput sequence, whose implementation requires nontrivial bit-operations. As an alternative, we introduce the quasi-regular golden ratio sequences, which are based on the fractional part of successive integer multiples of the golden ratio. By leveraging results from number theory, we show that point sets, which evenly cover the unit square or disc, can be computed by a simple incremental permutation of a generator golden ratio sequence. We compare ambient occlusion images generated with a Monte Carlo ray tracer based on random, Hammersley, blue noise, and golden ratio point sets. The source code of the ray tracer used for our experiments is available online at the address provided at the end of this article.

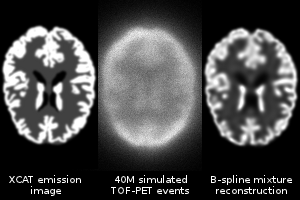
In emission tomography, images are usually represented by regular grids of voxels or overlapping smooth image elements (blobs). Few other image models have been proposed like tetrahedral meshes or point clouds that are adapted to an anatomical image. This work proposes a practical sparse and continuous image model inspired from the field of parametric density estimation for Gaussian mixture models. The position, size, aspect ratio and orientation of each image element is optimized as well as its weight with a very fast online estimation method. Furthermore, the number of mixture components, hence the image resolution, is locally adapted according to the available data. The system model is represented in the same basis as image elements and captures time of flight and positron range effects in an exact way. Computations use apodized B-spline approximations of Gaussians and simple closed-form analytical expressions without any sampling or interpolation. In consequence, the reconstructed image never suffers from spurious aliasing artifacts. Noiseless images of the XCAT brain phantom were reconstructed from simulated data.