Profile

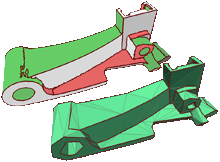
Aiming at robust surface structure recovery, we extend the powerful optimization technique of variational shape approximation by allowing for several different primitives to represent the geometric proxy of a surface region. While the original paper only considered planes, we also include spheres, cylinders, and more complex rollingball blend patches. The motivation for this choice is the fact that most technical CAD objects consist of patches from these four categories. The robust segmentation and global optimization properties which have been observed for the variational shape approximation carry over to our hybrid extension. Hence, we can use our algorithm to segment a given mesh model into characteristic patches and provide a corresponding geometric proxy for each patch. The expected result that we recover surface structures more robustly and thus obtain better approximations with a smaller number of primitives, is validated and demonstrated on a number of examples.

Surface splatting enables high quality and ecient rendering algorithms for dense point-sampled datasets. However, with increasing data complexity, the need for multiresolution models becomes evident. For triangle meshes, progressive or continuous level of detail hierarchies have proven to be very effective when it comes to (locally) adapt the resolution level of the 3D model to the application-dependent quality requirements. In this paper we transfer this concept to splat-based geometry representations. Our progressive splat decimation procedure uses the standard greedy approach but unlike previous work, it uses the full splat geometry in the decimation criteria and error estimates, not just the splat centers. With two improved error metrics, this new greedy framework offers better approximation quality than other progressive splat decimators. It comes even close to the recently proposed globally optimized single-resolution sub-sampling techniques while being faster by a factor of 3.

Allowing for copyright protection and ownership assertion, digital watermarking techniques, which have been successfully applied for classical media types like audio, images and videos, have recently been adapted for the newly emerged multimedia data type of 3D geometry models. In particular, the widely used spread-spectrum methods can be generalized for 3D datasets by transforming the original model to a frequency domain and perturbing the coefficients of the most dominant basis functions. Previous approaches employing this kind of spectral watermarking are mainly based on multiresolution mesh analysis, wavelet domain transformation or spectral mesh analysis. Though they already exhibit good resistance to many types of real-world attacks, they are often far too slow to cope with very large meshes due to their complicated numerical computations. In this paper, we present a novel spectral watermarking scheme using new orthogonal basis functions based on radial basis functions. With our proposed fast basis function orthogonalization, while observing similar persistence with respect to various attacks as other related approaches, our scheme runs faster by two orders of magnitude and thus can efficiently watermark very large models.

Using surface splats as a rendering primitive has gained increasing attention recently due to its potential for high-performance and high-quality rendering of complex geometric models. However, as with any other rendering primitive, the processing costs are still proportional to the number of primitives that we use to represent a given object. This is why complexity reduction for point-sampled geometry is as important as it is, e.g., for triangle meshes. In this paper we present a new sub-sampling technique for dense point clouds which is speccally adjusted to the particular geometric properties of circular or elliptical surface splats. A global optimization scheme computes an approximately minimal set of splats that covers the entire surface while staying below a globally prescribed maximum error tolerance e. Since our algorithm converts pure point sample data into surface splats with normal vectors and spatial extent, it can also be considered as a surface reconstruction technique which generates a hole-free piecewise linear C^(-1) continuous approximation of the input data. Here we can exploit the higher flexibility of surface splats compared to triangle meshes. Compared to previous work in this area we are able to obtain significantly lower splat numbers for a given error tolerance.

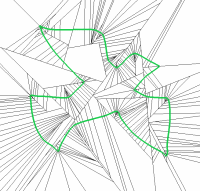
The signed distance field of a surface can effectively support many geometry processing tasks such as decimation, smoothing, and Boolean operations since it provides efficient access to distance (error) estimates. In this paper we present an algorithm to compute a piecewise linear, not necessarily continuous approximation of the signed distance field for a given object. Our approach is based on an adaptive hierarchical space partition that stores a linear distance function in every leaf node. We provide positive and negative criteria for selecting the splitting planes. Consequently the algorithm adapts the leaf cells of the space partition to the geometric shape of the underlying model better than previous methods. This results in a hierarchical representation with comparably low memory consumption and which allows for fast evaluation of the distance field function.

We present an out-of-core mesh decimation algorithm that is able to handle input and output meshes of arbitrary size. The algorithm reads the input from a data stream in a single pass and writes the output to another stream while using only a fixed-sized in-core buffer. By applying randomized multiple choice optimization, we are able to use incremental mesh decimation based on edge collapses and the quadric error metric. The quality of our results is comparable to state-of-the-art highquality mesh decimation schemes (which are slower than our algorithm) and the decimation performance matches the performance of the most efficient out-of-core techniques (which generate meshes of inferior quality).

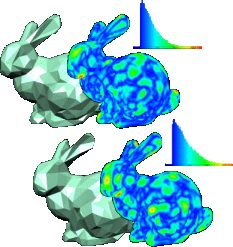
We present a new mesh decimation framework which is based on the probabilistic optimization technique of Multiple-Choice algorithms. While producing the same expected quality of the output meshes, the Multiple-Choice approach leads to a significant speed-up compared to the well-established standard framework for mesh decimation as a greedy optimization scheme. Moreover, Multiple-Choice decimation does not require a global priority queue data structure which reduces the memory overhead and simplifies the algorithmic structure. We explain why and how the Multiple- Choice optimization works well for the mesh decimation problem and give a detailed CPU profile analysis to explain where the speed-up comes from.