Profile

Pa­ra­met­ri­za­tion based methods have recently become very popular for the generation of high quality quad meshes. In contrast to previous approaches, they allow for intuitive user control in order to accommodate all kinds of application driven constraints and design intentions. A major obstacle in practice, however, are the relatively long computations that lead to response times of several minutes already for input models of moderate complexity. In this paper we introduce a novel strategy to handle highly complex input meshes with up to several millions of triangles such that quad meshes can still be created and edited within an interactive workflow. Our method is based on representing the input model on different levels of resolution with a mechanism to propagate pa­ra­met­ri­za­tions from coarser to finer levels. The major challenge is to guarantee consistent pa­ra­met­ri­za­tions even in the presence of charts, transition functions, and singularities. Moreover, the remaining degrees of freedom on coarser levels of resolution have to be chosen carefully in order to still achieve low distortion pa­ra­met­ri­za­tions. We demonstrate a prototypic system where the user can interactively edit quad meshes with powerful high-level operations such as guiding constraints, singularity repositioning, and singularity connections.

Various applications of global surface parametrization benefit from the alignment of parametrization isolines with principal curvature directions. This is particularly true for recent parametrization-based meshing approaches, where this directly translates into a shape-aware edge flow, better approximation quality, and reduced meshing artifacts. Existing methods to influence a parametrization based on principal curvature directions suffer from scale-dependence, which implies the necessity of parameter variation, or try to capture complex directional shape features using simple 1D curves. Especially for non-sharp features, such as chamfers, fillets, blends, and even more for organic variants thereof, these abstractions can be unfit. We present a novel approach which respects and exploits the 2D nature of such directional feature regions, detects them based on coherence and homogeneity properties, and controls the parametrization process accordingly. This approach enables us to provide an intuitive, scale-invariant control parameter to the user. It also allows us to consider non-local aspects like the topology of a feature, enabling further improvements. We demonstrate that, compared to previous approaches, global parametrizations of higher quality can be generated without user intervention.

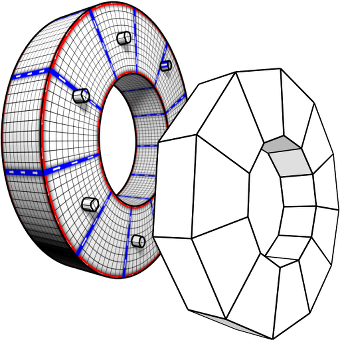
The most effective and popular tools for obtaining feature aligned quad meshes from triangular input meshes are based on cross field guided parametrization. These methods are incarnations of a conceptual three-step pipeline: (1) cross field computation, (2) field-guided surface parametrization, (3) quad mesh extraction. While in most meshing scenarios the user prescribes a desired target quad size or edge length, this information is typically taken into account from step 2 onwards only, but not in the cross field computation step. This turns into a problem in the presence of small scale geometric or topological features or noise in the input mesh: closely placed singularities are induced in the cross field, which are not properly reproducible by vertices in a quad mesh with the prescribed edge length, causing severe distortions or even failure of the meshing algorithm. We reformulate the construction of cross fields as well as field-guided parametrizations in a scale-aware manner which effectively suppresses densely spaced features and noise of geometric as well as topological kind. Dominant large-scale features are adequately preserved in the output by relying on the unaltered input mesh as the computational domain.

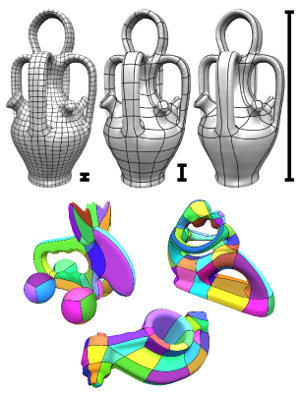
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths, state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts – a difficult task solely tackled by greedy methodologies before.

The most popular and actively researched class of quad remeshing techniques is the family of parametrization based quad meshing methods. They all strive to generate an integer-grid map, i.e. a parametrization of the input surface into R² such that the canonical grid of integer iso-lines forms a quad mesh when mapped back onto the surface in R³. An essential, albeit broadly neglected aspect of these methods is the quad extraction step, i.e. the materialization of an actual quad mesh from the mere “quad texture”. Quad (mesh) extraction is often believed to be a trivial matter but quite the opposite is true: Numerous special cases, ambiguities induced by numerical inaccuracies and limited solver precision, as well as imperfections in the maps produced by most methods (unless costly countermeasures are taken) pose significant challenges to the quad extractor. We present a method to sanitize a provided parametrization such that it becomes numerically consistent even in a limited precision floating point representation. Based on this we are able to provide a comprehensive and sound description of how to perform quad extraction robustly and without the need for any complex tolerance thresholds or disambiguation rules. On top of that we develop a novel strategy to cope with common local fold-overs in the parametrization. This allows our method, dubbed QEx, to generate all-quadrilateral meshes where otherwise holes, non-quad polygons or no output at all would have been produced. We thus enable the practical use of an entire class of maps that was previously considered defective. Since state of the art quad meshing methods spend a significant share of their run time solely to prevent local fold-overs, using our method it is now possible to obtain quad meshes significantly quicker than before. We also provide libQEx, an open source C++ reference implementation of our method and thus significantly lower the bar to enter the field of quad meshing.

We present a pipeline to generate high quality quad dominant meshes for vascular structures from a given volumetric image. As common for medical image segmentation we use a Level Set approach to separate the region of interest from the background. However in contrast to the standard method we control the topology of the deformable object – defined by the Level Set function – which allows us to extract a proper skeleton which represents the global topological information of the vascular structure. Instead of solving a complex global optimization problem to compute a quad mesh, we divide the problem and partition the complex model into junction and tube elements, employing the skeleton of the vascular structure. After computing quad meshes for the junctions using the Mixed Integer Quadrangulation approach, we re-mesh the tubes using an algorithm inspired by the well known Bresenham Algorithm for drawing lines which distributes irregular elements equally over the entire tube element.