Profile

|
Prof. Dr. David Bommes |
Publications
TinyAD: Automatic Differentiation in Geometry Processing Made Simple

Non-linear optimization is essential to many areas of geometry processing research. However, when experimenting with different problem formulations or when prototyping new algorithms, a major practical obstacle is the need to figure out derivatives of objective functions, especially when second-order derivatives are required. Deriving and manually implementing gradients and Hessians is both time-consuming and error-prone. Automatic differentiation techniques address this problem, but can introduce a diverse set of obstacles themselves, e.g. limiting the set of supported language features, imposing restrictions on a program's control flow, incurring a significant run time overhead, or making it hard to exploit sparsity patterns common in geometry processing. We show that for many geometric problems, in particular on meshes, the simplest form of forward-mode automatic differentiation is not only the most flexible, but also actually the most efficient choice. We introduce TinyAD: a lightweight C++ library that automatically computes gradients and Hessians, in particular of sparse problems, by differentiating small (tiny) sub-problems. Its simplicity enables easy integration; no restrictions on, e.g., looping and branching are imposed. TinyAD provides the basic ingredients to quickly implement first and second order Newton-style solvers, allowing for flexible adjustment of both problem formulations and solver details. By showcasing compact implementations of methods from parametrization, deformation, and direction field design, we demonstrate how TinyAD lowers the barrier to exploring non-linear optimization techniques. This enables not only fast prototyping of new research ideas, but also improves replicability of existing algorithms in geometry processing. TinyAD is available to the community as an open source library.
- Best Paper Award (1st place) at SGP 2022
- Graphics Replicability Stamp
» Show BibTeX
@article{schmidt2022tinyad,
title={{TinyAD}: Automatic Differentiation in Geometry Processing Made Simple},
author={Schmidt, Patrick and Born, Janis and Bommes, David and Campen, Marcel and Kobbelt, Leif},
year={2022},
journal={Computer Graphics Forum},
volume={41},
number={5},
}
Geodesic Distance Computation via Virtual Source Propagation

We present a highly practical, efficient, and versatile approach for computing approximate geodesic distances. The method is designed to operate on triangle meshes and a set of point sources on the surface. We also show extensions for all kinds of geometric input including inconsistent triangle soups and point clouds, as well as other source types, such as lines. The algorithm is based on the propagation of virtual sources and hence easy to implement. We extensively evaluate our method on about 10000 meshes taken from the Thingi10k and the Tet Meshing in the Wild data sets. Our approach clearly outperforms previous approximate methods in terms of runtime efficiency and accuracy. Through careful implementation and cache optimization, we achieve runtimes comparable to other elementary mesh operations (e.g. smoothing, curvature estimation) such that geodesic distances become a "first-class citizen" in the toolbox of geometric operations. Our method can be parallelized and we observe up to 6× speed-up on the CPU and 20× on the GPU. We present a number of mesh processing tasks easily implemented on the basis of fast geodesic distances. The source code of our method will be provided as a C++ library under the MIT license.
Note: we are currently in the process of cleaning up and documenting the source code. A basic implementation can already be found in the supplemental material.
Cost Minimizing Local Anisotropic Quad Mesh Refinement

Quad meshes as a surface representation have many conceptual advantages over triangle meshes. Their edges can naturally be aligned to principal curvatures of the underlying surface and they have the flexibility to create strongly anisotropic cells without causing excessively small inner angles. While in recent years a lot of progress has been made towards generating high quality uniform quad meshes for arbitrary shapes, their adaptive and anisotropic refinement remains difficult since a single edge split might propagate across the entire surface in order to maintain consistency. In this paper we present a novel refinement technique which finds the optimal trade-off between number of resulting elements and inserted singularities according to a user prescribed weighting. Our algorithm takes as input a quad mesh with those edges tagged that are prescribed to be refined. It then formulates a binary optimization problem that minimizes the number of additional edges which need to be split in order to maintain consistency. Valence 3 and 5 singularities have to be introduced in the transition region between refined and unrefined regions of the mesh. The optimization hence computes the optimal trade-off and places singularities strategically in order to minimize the number of consistency splits — or avoids singularities where this causes only a small number of additional splits. When applying the refinement scheme iteratively, we extend our binary optimization formulation such that previous splits can be undone if this prevents degenerate cells with small inner angles that otherwise might occur in anisotropic regions or in the vicinity of singularities. We demonstrate on a number of challenging examples that the algorithm performs well in practice.
» Show BibTeX
@article{Lyon:2020:Cost,
title = {Cost Minimizing Local Anisotropic Quad Mesh Refinement},
author = {Lyon, Max and Bommes, David and Kobbelt, Leif},
journal = {Computer Graphics Forum},
volume = {39},
number = {5},
year = {2020},
doi = {10.1111/cgf.14076}
}
Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing

The generation of quad meshes based on surface parametrization techniques has proven to be a versatile approach. These techniques quantize an initial seamless parametrization so as to obtain an integer grid map implying a pure quad mesh. State-of-the-art methods following this approach have to assume that the surface to be meshed either has no boundary, or has a boundary which the resulting mesh is supposed to be aligned to. In a variety of applications this is not desirable and non-boundary-aligned meshes or grid-parametrizations are preferred. We thus present a technique to robustly generate integer grid maps which are either boundary-aligned, non-boundary-aligned, or partially boundary-aligned, just as required by different applications. We thereby generalize previous work to this broader setting. This enables the reliable generation of trimmed quad meshes with partial elements along the boundary, preferable in various scenarios, from tiled texturing over design and modeling to fabrication and architecture, due to fewer constraints and hence higher overall mesh quality and other benefits in terms of aesthetics and flexibility.
@article{Lyon:2019:TrimmedQuadMeshing,
author = "Lyon, Max and Campen, Marcel and Bommes, David and Kobbelt, Leif",
title = "Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing",
journal = "ACM Transactions on Graphics",
volume = 38,
number = 4,
year = 2019
}
Singularity-Constrained Octahedral Fields for Hexahedral Meshing
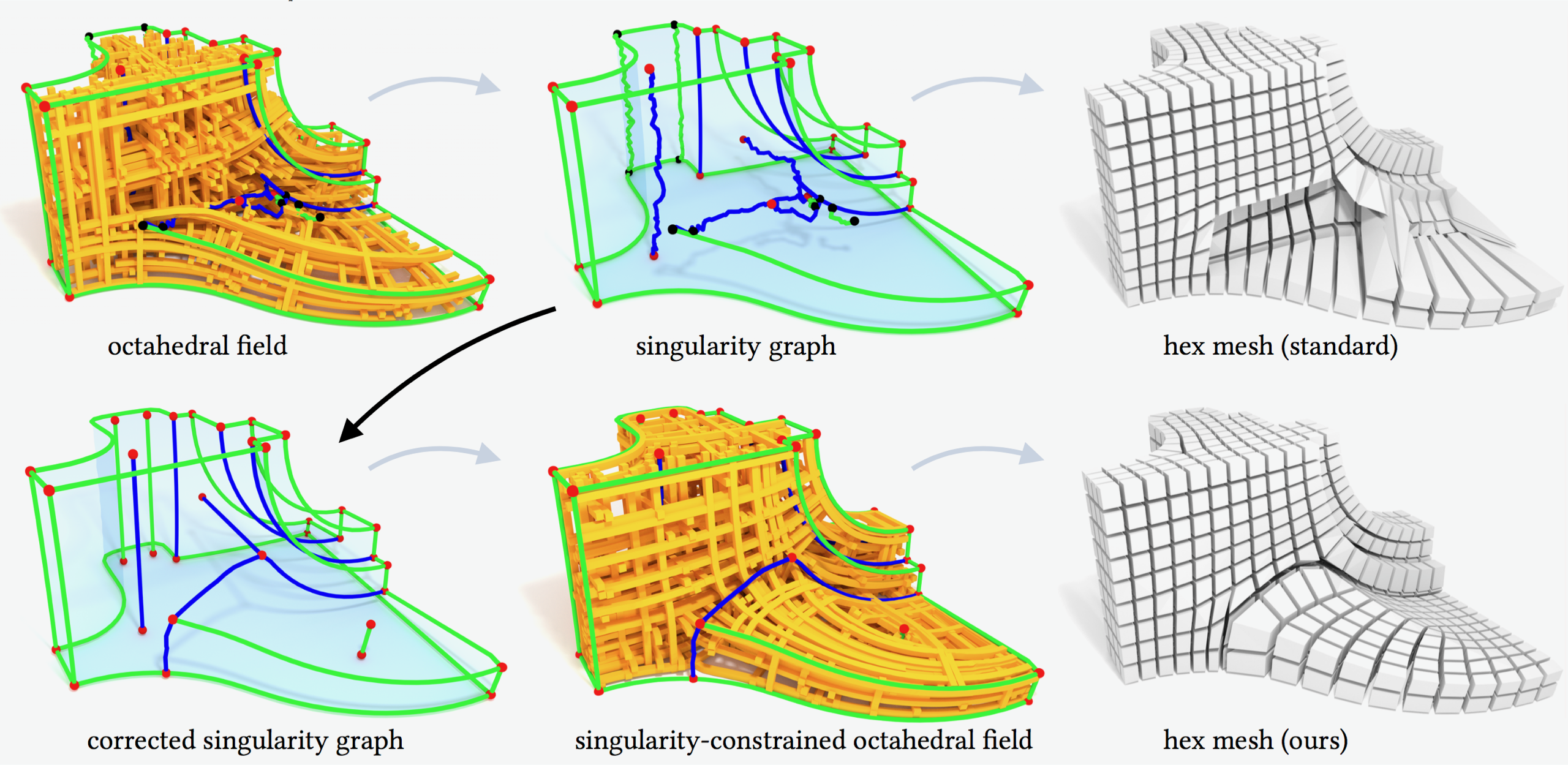
Despite high practical demand, algorithmic hexahedral meshing with guarantees on robustness and quality remains unsolved. A promising direction follows the idea of integer-grid maps, which pull back the Cartesian hexahedral grid formed by integer isoplanes from a parametric domain to a surface-conforming hexahedral mesh of the input object. Since directly optimizing for a high-quality integer-grid map is mathematically challenging, the construction is usually split into two steps: (1) generation of a surface-aligned octahedral field and (2) generation of an integer-grid map that best aligns to the octahedral field. The main robustness issue stems from the fact that smooth octahedral fields frequently exhibit singularity graphs that are not appropriate for hexahedral meshing and induce heavily degenerate integer-grid maps. The first contribution of this work is an enumeration of all local configurations that exist in hex meshes with bounded edge valence, and a generalization of the Hopf-Poincaré formula to octahedral fields, leading to necessary local and global conditions for the hex-meshability of an octahedral field in terms of its singularity graph. The second contribution is a novel algorithm to generate octahedral fields with prescribed hex-meshable singularity graphs, which requires the solution of a large non-linear mixed-integer algebraic system. This algorithm is an important step toward robust automatic hexahedral meshing since it enables the generation of a hex-meshable octahedral field.
Selective Padding for Polycube-based Hexahedral Meshing
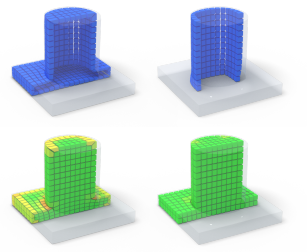
Abstract Hexahedral meshes generated from polycube mapping often exhibit a low number of singularities but also poor-quality elements located near the surface. It is thus necessary to improve the overall mesh quality, in terms of the minimum scaled Jacobian (MSJ) or average SJ (ASJ). Improving the quality may be obtained via global padding (or pillowing), which pushes the singularities inside by adding an extra layer of hexahedra on the entire domain boundary. Such a global padding operation suffers from a large increase of complexity, with unnecessary hexahedra added. In addition, the quality of elements near the boundary may decrease. We propose a novel optimization method which inserts sheets of hexahedra so as to perform selective padding, where it is most needed for improving the mesh quality. A sheet can pad part of the domain boundary, traverse the domain and form singularities. Our global formulation, based on solving a binary problem, enables us to control the balance between quality improvement, increase of complexity and number of singularities. We show in a series of experiments that our approach increases the MSJ value and preserves (or even improves) the ASJ, while adding fewer hexahedra than global padding.
@article{Cherchi2018SelectivePadding,
author = {Cherchi, G. and Alliez, P. and Scateni, R. and Lyon, M. and Bommes, D.},
title = {Selective Padding for Polycube-Based Hexahedral Meshing},
journal = {Computer Graphics Forum},
volume = {38},
number = {1},
pages = {580-591},
keywords = {computational geometry, modelling, physically based modelling, mesh generation, I.3.5 Computer Graphics: Computational Geometry and Object Modeling—Curve, surface, solid, and object representations},
doi = {https://doi.org/10.1111/cgf.13593},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.13593},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1111/cgf.13593},
abstract = {Abstract Hexahedral meshes generated from polycube mapping often exhibit a low number of singularities but also poor-quality elements located near the surface. It is thus necessary to improve the overall mesh quality, in terms of the minimum scaled Jacobian (MSJ) or average SJ (ASJ). Improving the quality may be obtained via global padding (or pillowing), which pushes the singularities inside by adding an extra layer of hexahedra on the entire domain boundary. Such a global padding operation suffers from a large increase of complexity, with unnecessary hexahedra added. In addition, the quality of elements near the boundary may decrease. We propose a novel optimization method which inserts sheets of hexahedra so as to perform selective padding, where it is most needed for improving the mesh quality. A sheet can pad part of the domain boundary, traverse the domain and form singularities. Our global formulation, based on solving a binary problem, enables us to control the balance between quality improvement, increase of complexity and number of singularities. We show in a series of experiments that our approach increases the MSJ value and preserves (or even improves) the ASJ, while adding fewer hexahedra than global padding.},
year = {2019}
}
Directional Field Synthesis, Design, and Processing

Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This course provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.
@inproceedings{Vaxman:2017:DFS:3084873.3084921,
author = {Vaxman, Amir and Campen, Marcel and Diamanti, Olga and Bommes, David and Hildebrandt, Klaus and Technion, Mirela Ben-Chen and Panozzo, Daniele},
title = {Directional Field Synthesis, Design, and Processing},
booktitle = {ACM SIGGRAPH 2017 Courses},
series = {SIGGRAPH '17},
year = {2017},
isbn = {978-1-4503-5014-3},
location = {Los Angeles, California},
pages = {12:1--12:30},
articleno = {12},
numpages = {30},
url = {http://doi.acm.org/10.1145/3084873.3084921},
doi = {10.1145/3084873.3084921},
acmid = {3084921},
publisher = {ACM},
address = {New York, NY, USA},
}
Boundary Element Octahedral Fields in Volumes
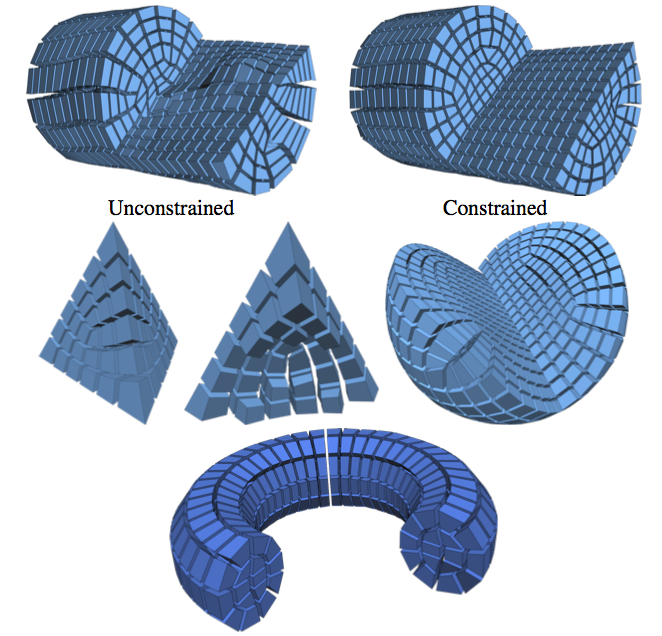
The computation of smooth fields of orthogonal directions within a volume is a critical step in hexahedral mesh generation, used to guide placement of edges and singularities. While this problem shares high-level structure with surface-based frame field problems, critical aspects are lost when extending to volumes, while new structure from the flat Euclidean metric emerges. Taking these considerations into account, this paper presents an algorithm for computing such “octahedral” fields. Unlike existing approaches, our formulation achieves infinite resolution in the interior of the volume via the boundary element method (BEM), continuously assigning frames to points in the interior from only a triangle mesh discretization of the boundary. The end result is an orthogonal direction field that can be sampled anywhere inside the mesh, with smooth variation and singular structure in the interior even with a coarse boundary. We illustrate our computed frames on a number of challenging test geometries. Since the octahedral frame field problem is relatively new, we also contribute a thorough discussion of theoretical and practical challenges unique to this problem.
@article{Solomon:2017:BEO:3087678.3065254,
author = {Solomon, Justin and Vaxman, Amir and Bommes, David},
title = {Boundary Element Octahedral Fields in Volumes},
journal = {ACM Trans. Graph.},
issue_date = {June 2017},
volume = {36},
number = {3},
month = may,
year = {2017},
issn = {0730-0301},
pages = {28:1--28:16},
articleno = {28},
numpages = {16},
url = {http://doi.acm.org/10.1145/3065254},
doi = {10.1145/3065254},
acmid = {3065254},
publisher = {ACM},
address = {New York, NY, USA},
keywords = {Octahedral fields, boundary element method, frames, singularity graph},
}
HexEx: Robust Hexahedral Mesh Extraction

State-of-the-art hex meshing algorithms consist of three steps: Frame-field design, parametrization generation, and mesh extraction. However, while the first two steps are usually discussed in detail, the last step is often not well studied. In this paper, we fully concentrate on reliable mesh extraction.
Parametrization methods employ computationally expensive countermeasures to avoid mapping input tetrahedra to degenerate or flipped tetrahedra in the parameter domain because such a parametrization does not define a proper hexahedral mesh. Nevertheless, there is no known technique that can guarantee the complete absence of such artifacts.
We tackle this problem from the other side by developing a mesh extraction algorithm which is extremely robust against typical imperfections in the parametrization. First, a sanitization process cleans up numerical inconsistencies of the parameter values caused by limited precision solvers and floating-point number representation. On the sanitized parametrization, we extract vertices and so-called darts based on intersections of the integer grid with the parametric image of the tetrahedral mesh. The darts are reliably interconnected by tracing within the parametrization and thus define the topology of the hexahedral mesh. In a postprocessing step, we let certain pairs of darts cancel each other, counteracting the effect of flipped regions of the parametrization. With this strategy, our algorithm is able to robustly extract hexahedral meshes from imperfect parametrizations which previously would have been considered defective. The algorithm will be published as an open source library.
@article{Lyon:2016:HexEx,
author = "Lyon, Max and Bommes, David and Kobbelt, Leif",
title = "HexEx: Robust Hexahedral Mesh Extraction",
journal = "ACM Transactions on Graphics",
volume = 35,
number = 4,
year = 2016
}
Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement

The typical goal of surface remeshing consists in finding a mesh that is (1) geometrically faithful to the original geometry, (2) as coarse as possible to obtain a low-complexity representation and (3) free of bad elements that would hamper the desired application. In this paper, we design an algorithm to address all three optimization goals simultaneously. The user specifies desired bounds on approximation error (delta), minimal interior angle (theta) and maximum mesh complexity N (number of vertices). Since such a desired mesh might not even exist, our optimization framework treats only the approximation error bound (delta) as a hard constraint and the other two criteria as optimization goals. More specifically, we iteratively perform carefully prioritized local operators, whenever they do not violate the approximation error bound and improve the mesh otherwise. Our optimization framework greedily searches for the coarsest mesh with minimal interior angle above (theta) and approximation error bounded by (delta). Fast runtime is enabled by a local approximation error estimation, while implicit feature preservation is obtained by specifically designed vertex relocation operators. Experiments show that our approach delivers high-quality meshes with implicitly preserved features and better balances between geometric fidelity, mesh complexity and element quality than the state-of-the-art.
@article{hu2016error,
title={Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement.},
author={Hu, K and Yan, DM and Bommes, D and Alliez, P and Benes, B},
journal={IEEE transactions on visualization and computer graphics},
year={2016}
}
Directional Field Synthesis, Design, and Processing
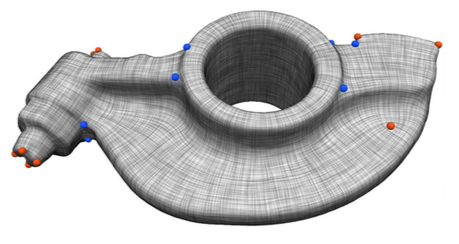
Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This report provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.
Geodesic Iso-Curve Signature
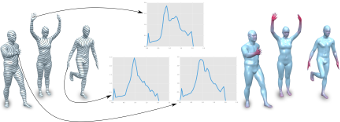
During the last decade a set of surface descriptors have been presented describing local surface features. Recent approaches have shown that augmenting local descriptors with topological information improves the correspondence and segmentation quality. In this paper we build upon the work of Tevs et al. and Sun and Abidi by presenting a surface descriptor which captures both local surface properties and topological features of 3D objects. We present experiments on shape repositories that are provided with ground-truth correspondences (FAUST, SCAPE, TOSCA) which show that this descriptor outperforms current local surface descriptors.
@INPROCEEDINGS{gbk2016,
author = {Gehre, Anne and Bommes, David and Kobbelt, Leif}
title = {Geodesic Iso-Curve Signature},
booktitle = {Vision, Modeling {\&} Visualization},
year = {2016},
publisher = {The Eurographics Association}
}
BendFields: Regularized Curvature Fields from Rough Concept Sketches
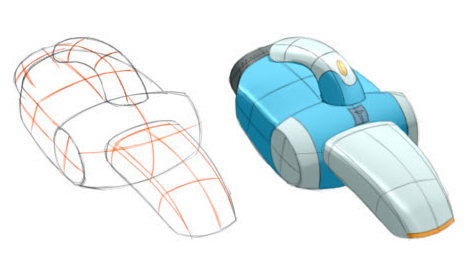
Designers frequently draw curvature lines to convey bending of smooth surfaces in concept sketches. We present a method to extrapolate curvature lines in a rough concept sketch, recovering the intended 3D curvature field and surface normal at each pixel of the sketch. This 3D information allows to enrich the sketch with 3D-looking shading and texturing. We first introduce the concept of regularized curvature lines that model the lines designers draw over curved surfaces, encompassing curvature lines and their extension as geodesics over flat or umbilical regions. We build on this concept to define the orthogonal cross field that assigns two regularized curvature lines to each point of a 3D surface. Our algorithm first estimates the projection of this cross field in the drawing, which is nonorthogonal due to foreshortening. We formulate this estimation as a scattered interpolation of the strokes drawn in the sketch, which makes our method robust to sketchy lines that are typical for design sketches. Our interpolation relies on a novel smoothness energy that we derive from our definition of regularized curvature lines. Optimizing this energy subject to the stroke constraints produces a dense nonorthogonal 2D cross field which we then lift to 3D by imposing orthogonality. Thus, one central concept of our approach is the generalization of existing cross field algorithms to the nonorthogonal case. We demonstrate our algorithm on a variety of concept sketches with various levels of sketchiness. We also compare our approach with existing work that takes clean vector drawings as input.
» Show BibTeX
@Article{IBB15,
author = "Iarussi, Emmanuel and Bommes, David and Bousseau, Adrien",
title = "BendFields: Regularized Curvature Fields from Rough Concept Sketches ",
journal = "ACM Transactions on Graphics",
year = "2015",
url = "http://www-sop.inria.fr/reves/Basilic/2015/IBB15"
}
Quantized Global Parametrization
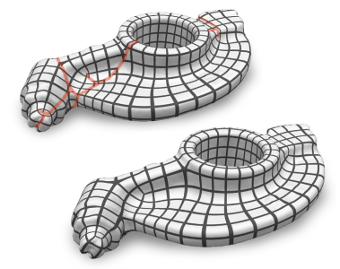
Global surface parametrization often requires the use of cuts or charts due to non-trivial topology. In recent years a focus has been on so-called seamless parametrizations, where the transition functions across the cuts are rigid transformations with a rotation about some multiple of 90 degrees. Of particular interest, e.g. for quadrilateral meshing, paneling, or texturing, are those instances where in addition the translational part of these transitions is integral (or more generally: quantized). We show that finding not even the optimal, but just an arbitrary valid quantization (one that does not imply parametric degeneracies), is a complex combinatorial problem. We present a novel method that allows us to solve it, i.e. to find valid as well as good quality quantizations. It is based on an original approach to quickly construct solutions to linear Diophantine equation systems, exploiting the specific geometric nature of the parametrization problem. We thereby largely outperform the state-of-the-art, sometimes by several orders of magnitude.
Level-of-Detail Quad Meshing
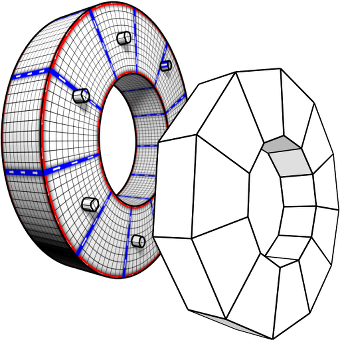
The most effective and popular tools for obtaining feature aligned quad meshes from triangular input meshes are based on cross field guided parametrization. These methods are incarnations of a conceptual three-step pipeline: (1) cross field computation, (2) field-guided surface parametrization, (3) quad mesh extraction. While in most meshing scenarios the user prescribes a desired target quad size or edge length, this information is typically taken into account from step 2 onwards only, but not in the cross field computation step. This turns into a problem in the presence of small scale geometric or topological features or noise in the input mesh: closely placed singularities are induced in the cross field, which are not properly reproducible by vertices in a quad mesh with the prescribed edge length, causing severe distortions or even failure of the meshing algorithm. We reformulate the construction of cross fields as well as field-guided parametrizations in a scale-aware manner which effectively suppresses densely spaced features and noise of geometric as well as topological kind. Dominant large-scale features are adequately preserved in the output by relying on the unaltered input mesh as the computational domain.
Integer-Grid Maps for Reliable Quad Meshing
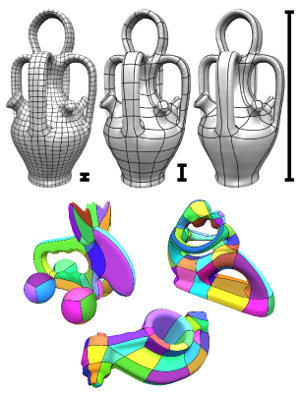
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths, state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts – a difficult task solely tackled by greedy methodologies before.
QEx: Robust Quad Mesh Extraction

The most popular and actively researched class of quad remeshing techniques is
the family of parametrization based quad meshing methods. They all strive
to generate an integer-grid map, i.e. a parametrization of the input surface
into R2 such that the canonical grid of integer iso-lines forms a
quad mesh when mapped back onto the surface in R3. An essential,
albeit broadly neglected aspect of these methods is the quad extraction
step, i.e. the materialization of an actual quad mesh from the mere “quad
texture”. Quad (mesh) extraction is often believed to be a trivial matter but
quite the opposite is true: Numerous special cases, ambiguities induced by
numerical inaccuracies and limited solver precision, as well as imperfections
in the maps produced by most methods (unless costly countermeasures are taken)
pose significant challenges to the quad extractor. We present a method to
sanitize a provided parametrization such that it becomes numerically
consistent even in a limited precision floating point representation. Based
on this we are able to provide a comprehensive and sound description of how to
perform quad extraction robustly and without the need for any complex
tolerance thresholds or disambiguation rules. On top of that we develop a
novel strategy to cope with common local fold-overs in the parametrization.
This allows our method, dubbed QEx, to generate all-quadrilateral meshes
where otherwise holes, non-quad polygons or no output at all would have been
produced. We thus enable the practical use of an entire class of maps that was
previously considered defective. Since state of the art quad meshing methods
spend a significant share of their run time solely to prevent local
fold-overs, using our method it is now possible to obtain quad meshes
significantly quicker than before. We also provide libQEx, an open source
C++ reference implementation of our method and thus significantly lower the
bar to enter the field of quad meshing.
Advanced Automatic Hexahedral Mesh Generation from Surface Quad Meshes

A purely topological approach for the generation of hexahedral meshes from quadrilateral surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage, the input surface mesh is reduced to a single hexahedron by successively eliminating loops from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination order. In this paper, we introduce several techniques to extend the scope of target shapes of the approach and significantly improve the quality of the generated hexahedral meshes. While the original method can only handle "almost convex" objects and requires mesh surgery and remeshing in case of concave geometry, we propose a method to overcome this issue by introducing the notion of concave dual loops. Furthermore, we analyze and improve the heuristic to determine the elimination order for the dual loops such that the inordinate introduction of interior singular edges, i.e. edges of degree other than four in the hexahedral mesh, can be avoided in many cases.
Dual Loops Meshing: Quality Quad Layouts on Manifolds
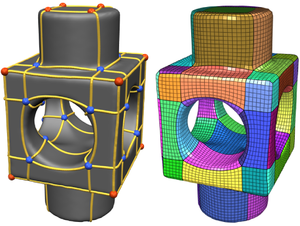
We present a theoretical framework and practical method for the automatic construction of simple, all-quadrilateral patch layouts on manifold surfaces. The resulting layouts are coarse, surface-embedded cell complexes well adapted to the geometric structure, hence they are ideally suited as domains and base complexes for surface parameterization, spline fitting, or subdivision surfaces and can be used to generate quad meshes with a high-level patch structure that are advantageous in many application scenarios. Our approach is based on the careful construction of the layout graph's combinatorial dual. In contrast to the primal this dual perspective provides direct control over the globally interdependent structural constraints inherent to quad layouts. The dual layout is built from curvature-guided, crossing loops on the surface. A novel method to construct these efficiently in a geometry- and structure-aware manner constitutes the core of our approach.
Rationalization of Triangle-Based Point-Folding Structures

In mechanical engineering and architecture, structural elements with low material consumption and high load-bearing capabilities are essential for light-weight and even self-supporting constructions. This paper deals with so called point-folding elements - non-planar, pyramidal panels, usually formed from thin metal sheets, which exploit the increased structural capabilities emerging from folds or creases. Given a triangulated free-form surface, a corresponding point-folding structure is a collection of pyramidal elements basing on the triangles. User-specified or material-induced geometric constraints often imply that each individual folding element has a different shape, leading to immense fabrication costs. We present a rationalization method for such structures which respects the prescribed aesthetic and production constraints and ?nds a minimal set of molds for the production process, leading to drastically reduced costs. For each base triangle we compute and parametrize the range of feasible folding elements that satisfy the given constraints within the allowed tolerances. Then we pose the rationalization task as a geometric intersection problem, which we solve so as to maximize the re-use of mold dies. Major challenges arise from the high precision requirements and the non-trivial parametrization of the search space. We evaluate our method on a number of practical examples where we achieve rationalization gains of more than 90%.
Practical Mixed-Integer Optimization for Geometry Processing
Proceedings of Curves and Surfaces 2010
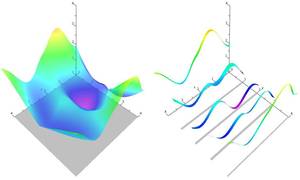
Solving mixed-integer problems, i.e., optimization problems where some of the unknowns are continuous while others are discrete, is NP-hard. Unfortunately, real-world problems like e.g., quadrangular remeshing usually have a large number of unknowns such that exact methods become unfeasible. In this article we present a greedy strategy to rapidly approximate the solution of large quadratic mixed-integer problems within a practically sufficient accuracy. The algorithm, which is freely available as an open source library implemented in C++, determines the values of the discrete variables by successively solving relaxed problems. Additionally the specification of arbitrary linear equality constraints which typically arise as side conditions of the optimization problem is possible. The performance of the base algorithm is strongly improved by two novel extensions which are (1) simultaneously estimating sets of discrete variables which do not interfere and (2) a fill-in reducing reordering of the constraints. Exemplarily the solver is applied to the problem of quadrilateral surface remeshing, enabling a great flexibility by supporting different types of user guidance within a real-time modeling framework for input surfaces of moderate complexity.
OpenVolumeMesh - A Versatile Index-Based Data Structure for 3D Polytopal Complexes
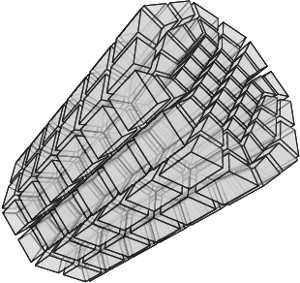
OpenVolumeMesh is a data structure which is able to represent heterogeneous 3-dimensional polytopal cell complexes and is general enough to also represent non- manifolds without incurring undue overhead. Extending the idea of half-edge based data structures for two-manifold surface meshes, all faces, i.e. the two-dimensional entities of a mesh, are represented by a pair of oriented half-faces. The concept of using directed half-entities enables inducing an orientation to the meshes in an intuitive and easy to use manner. We pursue the idea of encoding connectivity by storing first-order top-down incidence relations per entity, i.e. for each entity of dimension d, a list of links to the respective incident entities of dimension d?1 is stored. For instance, each half-face as well as its orientation is uniquely determined by a tuple of links to its incident half- edges or each 3D cell by the set of incident half-faces. This representation allows for handling non-manifolds as well as mixed-dimensional mesh configurations. No entity is duplicated according to its valence, instead, it is shared by all incident entities in order to reduce memory consumption. Furthermore, an array-based storage layout is used in combination with direct index-based access. This guarantees constant access time to the entities of a mesh. Although bottom-up incidence relations are implied by the top-down incidences, our data structure provides the option to explicitly generate and cache them in a transparent manner. This allows for accelerated navigation in the local neighbor- hood of an entity. We provide an open-source and platform-independent implementation of the proposed data structure written in C++ using dynamic typing paradigms. The li- brary is equipped with a set of STL compliant iterators, a generic property system to dynamically attach properties to all entities at run-time, and a serializer/deseri- alizer supporting a simple file format. Due to its similarity to the OpenMesh data structure, it is easy to use, in particular for those familiar with OpenMesh. Since the presented data structure is compact, intuitive, and efficient, it is suitable for a variety of applications, such as meshing, visualization, and numerical analysis. OpenVolumeMesh is open-source software licensed under the terms of the LGPL.
Global Structure Optimization of Quadrilateral Meshes

We introduce a fully automatic algorithm which optimizes the high-level structure of a given quadrilateral mesh to achieve a coarser quadrangular base complex. Such a topological optimization is highly desirable, since state-of-the-art quadrangulation techniques lead to meshes which have an appropriate singularity distribution and an anisotropic element alignment, but usually they are still far away from the high-level structure which is typical for carefully designed meshes manually created by specialists and used e.g. in animation or simulation. In this paper we show that the quality of the high-level structure is negatively affected by helical configurations within the quadrilateral mesh. Consequently we present an algorithm which detects helices and is able to remove most of them by applying a novel grid preserving simplification operator (GP-operator) which is guaranteed to maintain an all-quadrilateral mesh. Additionally it preserves the given singularity distribution and in particular does not introduce new singularities. For each helix we construct a directed graph in which cycles through the start vertex encode operations to remove the corresponding helix. Therefore a simple graph search algorithm can be performed iteratively to remove as many helices as possible and thus improve the high-level structure in a greedy fashion. We demonstrate the usefulness of our automatic structure optimization technique by showing several examples with varying complexity.
Mixed-Integer Quadrangulation
Proceedings of the 2009 SIGGRAPH Conference

We present a novel method for quadrangulating a given triangle mesh. After constructing an as smooth as possible symmetric cross field satisfying a sparse set of directional constraints (to capture the geometric structure of the surface), the mesh is cut open in order to enable a low distortion unfolding. Then a seamless globally smooth parametrization is computed whose iso-parameter lines follow the cross field directions. In contrast to previous methods, sparsely distributed directional constraints are sufficient to automatically determine the appropriate number, type and position of singularities in the quadrangulation. Both steps of the algorithm (cross field and parametrization) can be formulated as a mixed-integer problem which we solve very efficiently by an adaptive greedy solver. We show several complex examples where high quality quad meshes are generated in a fully automatic manner.
The Constrained Mixed-Integer Solver used in this project has been released under GPL and can be found on its projects page.
Quadrangular Parameterization for Reverse Engineering

The aim of Reverse Engineering is to convert an unstructured representation of a geometric object, emerging e.g. from laser scanners, into a natural, structured representation in the spirit of CAD models, which is suitable for numerical computations. Therefore we present a user-controlled, as isometric as possible parameterization technique which is able to prescribe geometric features of the input and produces high-quality quadmeshes with low distortion. Starting with a coarse, user-prescribed layout this is achieved by using affine functions for the transition between non-orthogonal quadrangular charts of a global parameterization. The shape of each chart is optimized non-linearly for isometry of the underlying parameterization to produce meshes with low edge-length distortion. To provide full control over the meshing alignment the user can additionally tag an arbitrary subset of the layout edges which are guaranteed to be represented by enforcing them to lie on iso-lines of the parameterization but still allowing the global parameterization to relax in the direction of the iso-lines.
Accurate Computation of Geodesic Distance Fields for Polygonal Curves on Triangle Meshes

We present an algorithm for the efficient and accurate computation of geodesic distance fields on triangle meshes. We generalize the algorithm originally proposed by Surazhsky et al. . While the original algorithm is able to compute geodesic distances to isolated points on the mesh only, our generalization can handle arbitrary, possibly open, polygons on the mesh to define the zero set of the distance field. Our extensions integrate naturally into the base algorithm and consequently maintain all its nice properties. For most geometry processing algorithms, the exact geodesic distance information is sampled at the mesh vertices and the resulting piecewise linear interpolant is used as an approximation to the true distance field. The quality of this approximation strongly depends on the structure of the mesh and the location of the medial axis of the distance fild. Hence our second contribution is a simple adaptive refinement scheme, which inserts new vertices at critical locations on the mesh such that the final piecewise linear interpolant is guaranteed to be a faithful approximation to the true geodesic distance field.
Efficient Linear System Solvers for Mesh Processing

Mario Botsch, David Bommes, Leif Kobbelt
The use of polygonal mesh representations for freeform geometry enables the formulation of many important geometry processing tasks as the solution of one or several linear systems. As a consequence, the key ingredient for efficient algorithms is a fast procedure to solve linear systems. A large class of standard problems can further be shown to lead more specifically to sparse, symmetric, and positive definite systems, that allow for a numerically robust and efficient solution. In this paper we discuss and evaluate the use of \emph{sparse direct solvers} for such kind of systems in geometry processing applications, since in our experiments they turned out to be superior even to highly optimized multigrid methods, but at the same time were considerably easier to use and implement. Although the methods we present are well known in the field of high performance computing, we observed that they are in practice surprisingly rarely applied to geometry processing problems.
GPU-based Tolerance Volumes for Mesh Processing

In an increasing number of applications triangle meshes represent a flexible and efficient alternative to traditional NURBS-based surface representations. Especially in engineering applications it is crucial to guarantee that a prescribed approximation tolerance to a given reference geometry is respected for any combination of geometric algorithms that are applied when processing a triangle mesh. We propose a simple and generic method for computing the distance of a given polygonal mesh to the reference surface, based on a linear approximation of its signed distance field. Exploiting the hardware acceleration of modern GPUs allows us to perform up to 3M triangle checks per second, enabling real-time distance evaluations even for complex geometries. An additional feature of our approach is the accurate high-quality distance visualization of dynamically changing meshes at a rate of 15M triangles per second. Due to its generality, the presented approach can be used to enhance any mesh processing method by global error control, guaranteeing the resulting mesh to stay within a prescribed error tolerance. The application examples that we present include mesh decimation, mesh smoothing and freeform mesh deformation.

