Profile

Although massive pre-trained vision-language models like CLIP show impressive generalization capabilities for many tasks, still it often remains necessary to fine-tune them for improved performance on specific datasets. When doing so, it is desirable that updating the model is fast and that the model does not lose its capabilities on data outside of the dataset, as is often the case with classical fine-tuning approaches. In this work we suggest a lightweight adapter that only updates the models predictions close to seen datapoints. We demonstrate the effectiveness and speed of this relatively simple approach in the context of few-shot learning, where our results both on classes seen and unseen during training are comparable with or improve on the state of the art.

The automatic creation of digital art has a long history in computer graphics. In this work, we focus on approximating input images to mimic artwork by the artist Kumi Yamashita, as well as the popular scribble art style. Both have in common that the artists create the works by using a single, contiguous thread (Yamashita) or stroke (scribble) that is placed seemingly at random when viewed at close range, but perceived as a tone-mapped picture when viewed from a distance. Our approach takes a rasterized image as input and creates a single, connected path by iteratively sampling a set of candidate segments that extend the current path and greedily selecting the best one. The candidates are sampled according to art style specific constraints, i.e. conforming to continuity constraints in the mathematical sense for the scribble art style. To model the perceptual discrepancy between close and far viewing distances, we minimize the difference between the input image and the image created by rasterizing our path after applying the contrast sensitivity function, which models how human vision blurs images when viewed from a distance. Our approach generalizes to colored images by using one path per color. We evaluate our approach on a wide range of input images and show that it is able to achieve good results for both art styles in grayscale and color.

Previous approaches to generate shapes in a 3D setting train a GAN on the latent space of an autoencoder (AE). Even though this produces convincing results, it has two major shortcomings. As the GAN is limited to reproduce the dataset the AE was trained on, we cannot reuse a trained AE for novel data. Furthermore, it is difficult to add spatial supervision into the generation process, as the AE only gives us a global representation. To remedy these issues, we propose to train the GAN on grids (i.e. each cell covers a part of a shape). In this representation each cell is equipped with a latent vector provided by an AE. This localized representation enables more expressiveness (since the cell-based latent vectors can be combined in novel ways) as well as spatial control of the generation process (e.g. via bounding boxes). Our method outperforms the current state of the art on all established evaluation measures, proposed for quantitatively evaluating the generative capabilities of GANs. We show limitations of these measures and propose the adaptation of a robust criterion from statistical analysis as an alternative.

State of the art quadrangulation methods are able to reliably and robustly convert triangle meshes into quad meshes. Most of these methods rely on a dense direction field that is used to align a parametrization from which a quad mesh can be extracted. In this context, the aforementioned direction field is of particular importance, as it plays a key role in determining the structure of the generated quad mesh. If there are no user-provided directions available, the direction field is usually interpolated from a subset of principal curvature directions. To this end, a number of heuristics that aim to identify significant surface regions have been proposed. Unfortunately, the resulting fields often fail to capture the structure found in meshes created by human experts. This is due to the fact that experienced designers can leverage their domain knowledge in order to optimize a mesh for a specific application. In the context of physics simulation, for example, a designer might prefer an alignment and local refinement that facilitates a more accurate numerical simulation. Similarly, a character artist may prefer an alignment that makes the resulting mesh easier to animate. Crucially, this higher level domain knowledge cannot be easily extracted from local curvature information alone. Motivated by this issue, we propose a data-driven approach to the computation of direction fields that allows us to mimic the structure found in existing meshes, which could originate from human experts or other sources. More specifically, we make use of a neural network that aggregates global and local shape information in order to compute a direction field that can be used to guide a parametrization-based quad meshing method. Our approach is a first step towards addressing this challenging problem with a fully automatic learning-based method. We show that compared to classical techniques our data-driven approach combined with a robust model-driven method, is able to produce results that more closely exhibit the ground truth structure of a synthetic dataset (i.e. a manually designed quad mesh template fitted to a variety of human body types in a set of different poses).

We propose a novel method to synthesize geometric models from a given class of context-aware structured shapes such as buildings and other man-made objects. Our central idea is to leverage powerful machine learning methods from the area of natural language processing for this task. To this end, we propose a technique that maps shapes to strings and vice versa, through an intermediate shape graph representation. We then convert procedurally generated shape repositories into text databases that in turn can be used to train a variational autoencoder which enables higher level shape manipulation and synthesis like, e.g., interpolation and sampling via its continuous latent space.

Automatic synthesis of high quality 3D shapes is an ongoing and challenging area of research. While several data-driven methods have been proposed that make use of neural networks to generate 3D shapes, none of them reach the level of quality that deep learning synthesis approaches for images provide. In this work we present a method for a convolutional point cloud decoder/generator that makes use of recent advances in the domain of image synthesis. Namely, we use Adaptive Instance Normalization and offer an intuition on why it can improve training. Furthermore, we propose extensions to the minimization of the commonly used Chamfer distance for auto-encoding point clouds. In addition, we show that careful sampling is important both for the input geometry and in our point cloud generation process to improve results. The results are evaluated in an auto-encoding setup to offer both qualitative and quantitative analysis. The proposed decoder is validated by an extensive ablation study and is able to outperform current state of the art results in a number of experiments. We show the applicability of our method in the fields of point cloud upsampling, single view reconstruction, and shape synthesis.

Feature curves on 3D shapes provide important hints about significant parts of the geometry and reveal their underlying structure. However, when we process real world data, automatically detected feature curves are affected by measurement uncertainty, missing data, and sampling resolution, leading to noisy, fragmented, and incomplete feature curve networks. These artifacts make further processing unreliable. In this paper we analyze the global co-occurrence information in noisy feature curve networks to fill in missing data and suppress weakly supported feature curves. For this we propose an unsupervised approach to find meaningful structure within the incomplete data by detecting multiple occurrences of feature curve configurations (co-occurrence analysis). We cluster and merge these into feature curve templates, which we leverage to identify strongly supported feature curve segments as well as to complete missing data in the feature curve network. In the presence of significant noise, previous approaches had to resort to user input, while our method performs fully automatic feature curve co-completion. Finding feature reoccurrences however, is challenging since naive feature curve comparison fails in this setting due to fragmentation and partial overlaps of curve segments. To tackle this problem we propose a robust method for partial curve matching. This provides us with the means to apply symmetry detection methods to identify co-occurring configurations. Finally, Bayesian model selection enables us to detect and group re-occurrences that describe the data well and with low redundancy.

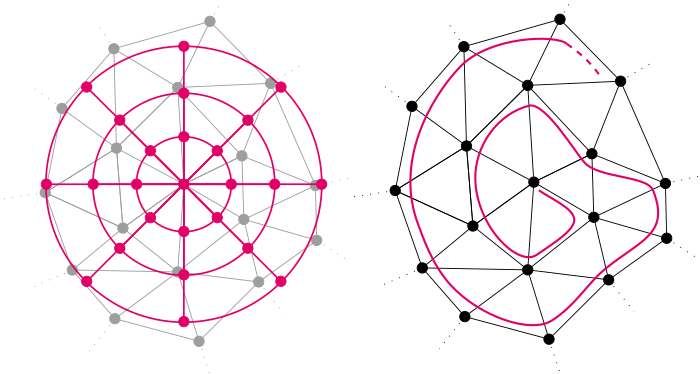
The question of representation of 3D geometry is of vital importance when it comes to leveraging the recent advances in the field of machine learning for geometry processing tasks. For common unstructured surface meshes state-of-the-art methods rely on patch-based or mapping-based techniques that introduce resampling operations in order to encode neighborhood information in a structured and regular manner. We investigate whether such resampling can be avoided, and propose a simple and direct encoding approach. It does not only increase processing efficiency due to its simplicity - its direct nature also avoids any loss in data fidelity. To evaluate the proposed method, we perform a number of experiments in the challenging domain of intrinsic, non-rigid shape correspondence estimation. In comparisons to current methods we observe that our approach is able to achieve highly competitive results.

Feature curves on surface meshes are usually defined solely based on local shape properties such as dihedral angles and principal curvatures. From the application perspective, however, the meaningfulness of a network of feature curves also depends on a global scale parameter that takes the distance between feature curves into account, i.e., on a coarse scale, nearby feature curves should be merged or suppressed if the surface region between them is not representable at the given scale/resolution. In this paper, we propose a computational approach to the intuitive notion of scale conforming feature curve networks where the density of feature curves on the surface adapts to a global scale parameter. We present a constrained global optimization algorithm that computes scale conforming feature curve networks by eliminating curve segments that represent surface features, which are not compatible to the prescribed scale. To demonstrate the usefulness of our approach we apply isotropic and anisotropic remeshing schemes that take our feature curve networks as input. For a number of example meshes, we thus generate high quality shape approximations at various levels of detail.

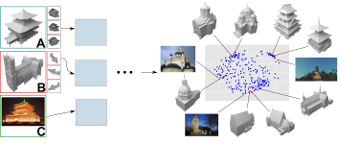
We present a method that expands on previous work in learning human perceived style similarity across objects with different structures and functionalities. Unlike previous approaches that tackle this problem with the help of hand-crafted geometric descriptors, we make use of recent advances in metric learning with neural networks (deep metric learning). This allows us to train the similarity metric on a shape collection directly, since any low- or high-level features needed to discriminate between different styles are identified by the neural network automatically. Furthermore, we avoid the issue of finding and comparing sub-elements of the shapes. We represent the shapes as rendered images and show how image tuples can be selected, generated and used efficiently for deep metric learning. We also tackle the problem of training our neural networks on relatively small datasets and show that we achieve style classification accuracy competitive with the state of the art. Finally, to reduce annotation effort we propose a method to incorporate heterogeneous data sources by adding annotated photos found online in order to expand or supplant parts of our training data.

A purely topological approach for the generation of hexahedral meshes from quadrilateral surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage, the input surface mesh is reduced to a single hexahedron by successively eliminating loops from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination order. In this paper, we introduce several techniques to extend the scope of target shapes of the approach and significantly improve the quality of the generated hexahedral meshes. While the original method can only handle "almost convex" objects and requires mesh surgery and remeshing in case of concave geometry, we propose a method to overcome this issue by introducing the notion of concave dual loops. Furthermore, we analyze and improve the heuristic to determine the elimination order for the dual loops such that the inordinate introduction of interior singular edges, i.e. edges of degree other than four in the hexahedral mesh, can be avoided in many cases.