Profile

|
Dr. Stephan Bischoff |
Publications
Geometric Modeling Based on Polygonal Meshes

In the last years triangle meshes have become increasingly popular and are nowadays intensively used in many different areas of computer graphics and geometry processing. In classical CAGD irregular triangle meshes developed into a valuable alternative to traditional spline surfaces, since their conceptual simplicity allows for more flexible and highly efficient processing. Moreover, the consequent use of triangle meshes as surface representation avoids error-prone conversions, e.g., from CAD surfaces to mesh-based input data of numerical simulations. Besides classical geometric modeling, other major areas frequently employing triangle meshes are computer games and movie production. In this context geometric models are often acquired by 3D scanning techniques and have to undergo post-processing and shape optimization techniques before being actually used in production.
Extracting consistent and manifold interfaces from multi-valued volume data sets
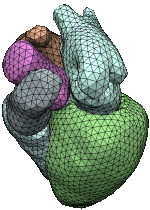
We propose an algorithm to construct a set of interfaces that separate the connected components of a multi-valued volume dataset. While each single interface is a manifold triangle mesh, two or more interfaces may join consistently along their common boundaries, i.e. there are no T-junctions or gaps. In contrast to previous work, our algorithm classifies and removes the topological ambiguities from the volume before extracting the interfaces. This not only allows for a simple and stable extraction algorithm, but also makes it possible to include user constraints.
Structure Preserving CAD Model Repair

There are two major approaches for converting a tessellated CAD model that contains inconsistencies like cracks or intersections into a manifold and closed triangle mesh. Surface oriented algorithms try to fix the inconsistencies by perturbing the input only slightly, but they often cannot handle special cases. Volumetric algorithms on the other hand produce guaranteed manifold meshes but mostly destroy the structure of the input tessellation due to global resampling. In this paper we combine the advantages of both approaches: We exploit the topological simplicity of a voxel grid to reconstruct a cleaned up surface in the vicinity of intersections and cracks, but keep the input tessellation in regions that are away from these inconsistencies. We are thus able to preserve any characteristic structure (i.e. iso-parameter or curvature lines) that might be present in the input tessellation. Our algorithm closes gaps up to a user-defined maximum diameter, resolves intersections, handles incompatible patch orientations and produces a feature-sensitive, manifold output that stays within a prescribed error-tolerance to the input model.
Automatic Restoration of Polygon Models

We present a fully automatic technique which converts an inconsistent input mesh into an output mesh that is guaranteed to be a clean and consistent mesh representing the closed manifold surface of a solid object. The algorithm removes all typical mesh artifacts such as degenerate triangles, incompatible face orientation, non-manifold vertices and edges, overlapping and penetrating polygons, internal redundant geometry as well as gaps and holes up to a user-defined maximum size. Moreover, the output mesh always stays within a prescribed tolerance to the input mesh. Due to the effective use of a hierarchical octree data structure, the algorithm achieves high voxel resolution (up to 4096^3 on a 2GB PC) and processing times of just a few minutes for moderately complex objects. We demonstrate our technique on various architectural CAD models to show its robustness and reliability.
Snakes on triangle meshes

In this work we introduce a new method for representing and evolving snakes that are constrained to lie on a prescribed surface (triangle mesh). The new representation allows to automatically adapt the snake resolution to the surface tesselation and does not need any (unstable) back-projection operations. Furthermore, it enables efficient and robust collision detection and gives us complete control on the topological behaviour of the snakes, i.e. snakes may split or merge depending on the intended task. Possible applications include enhanced mesh scissoring operations and the detection of constrictions of a surface.
Teaching meshes, subdivision and multiresolution techniques

In recent years, geometry processing algorithms that directly operate on polygonal meshes have become an indispensable tool in computer graphics, CAD/CAM applications, numerical simulations, and medical imaging. Because the demand for people that are specialized in these techniques increases steadily the topic is finding its way into the standard curricula of related lectures on computer graphics and geometric modeling and is often the subject of seminars and presentations. In this article we suggest a toolbox to educators who are planning to set up a lecture or talk about geometry processing for a specific audience. For this we propose a set of teaching blocks, each of which covers a specific subtopic. These teaching blocks can be assembled so as to fit different occasions like lectures, courses, seminars and talks and different audiences like students and industrial practitioners. We also provide examples that can be used to deepen the subject matter and give references to the most relevant work.
Parameterization-free active contour models

We present a novel approach for representing and evolving deformable active contours by restricting the movement of the contour vertices to the grid-lines of a uniform lattice. This restriction implicitly controls the (re-) parameterization of the contour and hence makes it possible to employ parameterization independent evolution rules. Moreover, the underlying uniform grid makes self-collision detection very efficient. Our contour model is also able to perform topology changes but - more importantly - it can detect and handle self-collisions at sub-pixel precision. In applications where topology changes are not appropriate we generate contours that touch themselves without any gaps or self-intersections.
Topologically Correct Extraction of the Cortical Surface of a Brain Using Level-Set Methods

In this paper we present a level-set framework for accurate and efficient extraction of the surface of a brain from MRI data. To prevent the so-called partial volume effect we use a topology preserving model that ensures the correct topology of the surface at all times during the reconstruction process. We also describe improvements that enhance its stability, accuracy and efficiency. The resulting reconstruction can then be used in downstream applications where we in particular focus on the problem of accurately measuring geodesic distances on the surface.
Sub-Voxel Topology Control for Level Set Surfaces
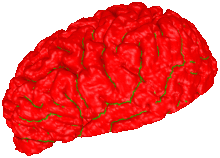
Active contour models are an efficient, accurate, and robust tool for the segmentation of 2D and 3D image data. In particular, geometric deformable models (GDM) that represent an active contour as the level set of an implicit function have proven to be very effective. GDMs, however, do not provide any topology control, i.e. contours may merge or split arbitrarily and hence change the genus of the reconstructed surface. This behavior is inadequate in settings like the segmentation of organic tissue or other objects whose genus is known beforehand. In this paper we describe a novel method to overcome this limitation while still preserving the favorable properties of the GDM setup. We achieve this by adding (sparse) topological information to the volume representation at locations where it is necessary to locally resolve topological ambiguities. Since the sparse topology information is attached to the edges of the voxel grid, we can reconstruct the interfaces where the deformable surface touches itself at sub-voxel accuracy. We also demonstrate the efficiency and robustness of our method on synthetic as well as on real (MRT) scan data.
Isosurface Reconstruction with Topology Control
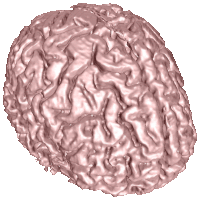
Extracting isosurfaces from volumetric datasets is an essential step for indirect volume rendering algorithms. For physically measured data like it is used, e.g. in medical imaging applications one often introduces topological errors such as small handles that stem from measurement inaccuracy and cavities that are generated by tight folds of an organ. During isosurface extraction these measurement errors result in a surface whose genus is much higher than that of the actual surface. In many cases however, the topological type of the object under consideration is known beforehand, e.g., the cortex of a human brain is always homeomorphic to a sphere. By using topology preserving morphological operators we can exploit this knowledge to gradually dilate an initial set of voxels with correct topology until it fits the target isosurface. This approach avoids the formation of handles and cavities and guarantees a topologically correct reconstruction of the object's surface.
Streaming 3D Geometry Data Over Lossy Communication Channels
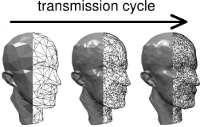
In this paper we propose a progressive 3D geometry transmission technique that is robust with respect to data loss. In a preprocessing step we decompose a given polygon mesh model into a set of overlapping ellipsoids, representing the coarse shape of the model, and a stream of sample points, representing its fine detail. On the client-side, we derive a coarse approximation of the model from the ellipsoid decomposition and then re-insert the sample points to reconstruct the fine detail. The overlapping ellipsoids as well as the sample points represent independent pieces of geometric information, hence partial data loss can be tolerated by our reconstruction algorithm and will only lead to a gradual degradation of the reconstruction quality. We present a transmission scheme that is especially well-suited for geometry broadcasting where we exploit that the order of the sample points can be arbitrarily permuted.
Ellipsoid decomposition of 3D-models

In this paper we present a simple technique to approximate the volume enclosed by a given triangle mesh with a set of overlapping ellipsoids. This type of geometry representation allows us to approximately reconstruct 3D-shapes from a very small amount of information being transmitted. The two central questions that we address are: how can we compute optimal fitting ellipsoids that lie in the interior of a given triangle mesh and how do we select the most significant (least redundant) subset from a huge number of candidate ellipsoids. Our major motivation for computing ellipsoid decompositions is the robust transmission of geometric objects where the receiver can reconstruct the 3D-shape even if part of the data gets lost during transmission.
Towards Robust Broadcasting of Geometry Data

We present new algorithms for the robust transmission of geometric data sets, i.e. transmission which allows the receiver to recover (an approximation of) the original geometric object even if parts of the data get lost on the way. These algorithms can be considered as hinted point cloud triangulation schemes since the general manifold reconstruction problem is simplified by adding tags to the vertices and by providing a coarse base-mesh which determines the global surface topology. Robust transmission techniques exploit the geometric coherence of the data and do not require redundant transmission protocols on lower software layers. As an example application scenario we describe the teletext-like broadcasting of 3D models.
OpenMesh -- a generic and efficient polygon mesh data structure
We describe the implementation of a half-edge data structure for the static representation and dynamic handling of arbitrary polygonal meshes. The particular design of the data structures and classes aims at maximum flexibility and high performance. We achieve this by using generative programming concepts which allow the compiler to resolve most of the special case handling decisions at compile time. We evaluate our data structure based on prototypic implementations of mesh processing applications such as decimation and smoothing.
An implementation is available in the Software section.
Towards Hardware Implementation Of Loop Subdivision

We present a novel algorithm to evaluate and render Loop subdivision surfaces. The algorithm exploits the fact that Loop subdivision surfaces are piecewise polynomial and uses the forward difference technique for efficiently computing uniform samples on the limit surface. The main advantage of our algorithm is that it only requires a small and constant amount of memory that does not depend on the subdivision depth. The simple structure of the algorithm enables a scalable degree of hardware implementation. By low-level parallelization of the computations, we can reduce the critical computation costs to a theoretical minimum of about one float[3]-operation per triangle.
Geometric Modeling Based on Polygonal Meshes

While traditional computer aided design (CAD) is mainly based on piecewise polynomial surface representations, the recent advances in the efficient handling of polygonal meshes have made available a set of powerful techniques which enable sophisticated modeling operations on freeform shapes. In this tutorial we are going to give a detailed introduction into the various techniques that have been proposed over the last years. Those techniques address important issues such as surface generation from discrete samples (e.g. laser scans) or from control meshes (ab initio design); complexity control by adjusting the level of detail of a given 3D-model to the current application or to the available hardware resources; advanced mesh optimization techniques that are based on the numerical simulation of physical material (e.g. membranes or thin plates) and finally the generation and modification of hierarchical representations which enable sophisticated multiresolution modeling functionality. We present an interactive system for the generation of high quality triangle meshes that allows us to handle hybrid geometry (point clouds, polygons,...) as input data. In order to be able to robustly process huge data sets, we exploit graphics hardware features like the raster manager and the z-buffer for specific sub-tasks in the overall procedure. By this we significantly accelerate the stitching of mesh patches and obtain an algorithm for sub-sampling the data points in linear time. The target resolution and the triangle alignment in sub-regions of the resulting mesh can be controlled by adjusting the screen resolution and viewing transformation. An intuitive user interface provides a flexible tool for application dependent optimization of the mesh.

