Profile

|
Presentations
Event |
Type |
Title |
|---|---|---|
| INRIA-Sophia Antipolis (GEOMETRICA/TITANE Seminar) | Invited Talk | Geometry Optimization for Dual-Layer Support Structures |
| IEEE CVPR 2013 | Poster | Efficient Computation of Shortest Path-Concavity for 3D Meshes |
| Advances in Architectural Geometry (AAG) 2012 | Paper | Variational Tangent Plane Intersection for Planar Polygonal Meshing |
| Eurographics 2012 | Paper | Rationalization of Triangle-Based Point-Folding Structures |
Publications
Zometool Shape Approximation

We present an algorithm that approximates 2-manifold surfaces with Zometool models while preserving their topology. Zometool is a~popular hands-on mathematical modeling system used in teaching, research and for recreational model assemblies at home. This construction system relies on a single node type with a small, fixed set of directions and only 9 different edge types in its basic form. While being naturally well suited for modeling symmetries, various polytopes or visualizing molecular structures, the inherent discreteness of the system poses difficult constraints on any algorithmic approach to support the modeling of freeform shapes. We contribute a set of local, topology preserving Zome mesh modification operators enabling the efficient exploration of the space of 2-manifold Zome models around a given input shape. Starting from a rough initial approximation, the operators are iteratively selected within a stochastic framework guided by an energy functional measuring the quality of the approximation. We demonstrate our approach on a number of designs and also describe parameters which are used to explore different complexities and enable coarse approximations.
Interactive Volume-Based Visualization and Exploration for Diffusion Fiber Tracking
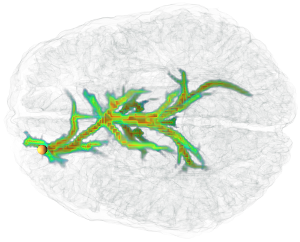
We present a new method to interactively compute and visualize fiber bundles extracted from a diffusion magnetic resonance image. It uses Dijkstra's shortest path algorithm to find globally optimal pathways from a given seed to all other voxels. Our distance function enables Dijkstra to generalize to larger voxel neighborhoods, resulting in fewer quantization artifacts of the orientations, while the shortest paths are still efficiently computable. Our volumetric fiber representation enables the usage of volume rendering techniques. Therefore no complicated pruning or analysis of the resulting fiber tree is needed in order to visualize important fibers. In fact, this can efficiently be done by changing a transfer function. Our application is highly interactive, allowing the user to focus completely on the exploration of the data.
Zometool Rationalization of Freeform Surfaces
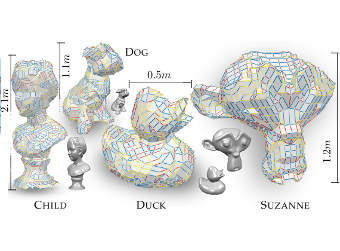
An ever broader availability of freeform designs together with an increasing demand for product customization has lead to a rising interest in efficient physical realization of such designs, the trend toward personal fabrication. Not only large-scale architectural applications are (becoming increasingly) popular but also different consumer-level rapid-prototyping applications, including toy and 3D puzzle creation. In this work we present a method for do-it-yourself reproduction of freeform designs without the typical limitation of state-of-the-art approaches requiring manufacturing custom parts using semi-professional laser cutters or 3d printers. Our idea is based on a popular mathematical modeling system (Zometool) commonly used for modeling higher dimensional polyhedra and symmetric structures such as molecules and crystal lattices. The proposed method extends the scope of Zometool modeling to freeform, disk-topology surfaces. While being an efficient construction system on the one hand (consisting only of a single node type and 9 different edge types), this inherent discreteness of the Zometool system, on the other hand gives rise to a hard approximation problem. We base our method on a marching front approach, where elements are not added in a greedy sense, but rather whole regions on the front are filled optimally, using a set of problem specific heuristics to keep complexity under control.
Efficient Computation of Shortest Path-Concavity for 3D Meshes
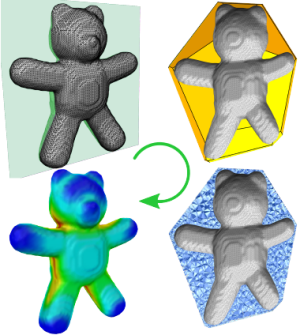
In the context of shape segmentation and retrieval object-wide distributions of measures are needed to accurately evaluate and compare local regions of shapes. Lien et al. proposed two point-wise concavity measures in the context of Approximate Convex Decompositions of polygons measuring the distance from a point to the polygon’s convex hull: an accurate Shortest Path-Concavity (SPC) measure and a Straight Line-Concavity (SLC) approximation of the same. While both are practicable on 2D shapes, the exponential costs of SPC in 3D makes it inhibitively expensive for a generalization to meshes. In this paper we propose an efficient and straight forward approximation of the Shortest Path-Concavity measure to 3D meshes. Our approximation is based on discretizing the space between mesh and convex hull, thereby reducing the continuous Shortest Path search to an efficiently solvable graph problem. Our approach works out-of-the-box on complex mesh topologies and requires no complicated handling of genus. Besides presenting a rigorous evaluation of our method on a variety of input meshes, we also define an SPC-based Shape Descriptor and show its superior retrieval and runtime performance compared with the recently presented results on the Convexity Distribution by Lian et al.
Rationalization of Triangle-Based Point-Folding Structures

In mechanical engineering and architecture, structural elements with low material consumption and high load-bearing capabilities are essential for light-weight and even self-supporting constructions. This paper deals with so called point-folding elements - non-planar, pyramidal panels, usually formed from thin metal sheets, which exploit the increased structural capabilities emerging from folds or creases. Given a triangulated free-form surface, a corresponding point-folding structure is a collection of pyramidal elements basing on the triangles. User-specified or material-induced geometric constraints often imply that each individual folding element has a different shape, leading to immense fabrication costs. We present a rationalization method for such structures which respects the prescribed aesthetic and production constraints and ?nds a minimal set of molds for the production process, leading to drastically reduced costs. For each base triangle we compute and parametrize the range of feasible folding elements that satisfy the given constraints within the allowed tolerances. Then we pose the rationalization task as a geometric intersection problem, which we solve so as to maximize the re-use of mold dies. Major challenges arise from the high precision requirements and the non-trivial parametrization of the search space. We evaluate our method on a number of practical examples where we achieve rationalization gains of more than 90%.
Variational Tangent Plane Intersection for Planar Polygonal Meshing
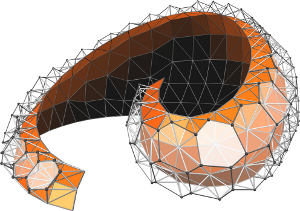
Several theoretical and practical geometry applications are based on polygon meshes with planar faces. The planar panelization of freeform surfaces is a prominent example from the field of architectural geometry. One approach to obtain a certain kind of such meshes is by intersection of suitably distributed tangent planes. Unfortunately, this simple tangent plane intersection (TPI) idea is limited to the generation of hex-dominant meshes: as vertices are in general defined by three intersecting planes, the resulting meshes are basically duals of triangle meshes.
The explicit computation of intersection points furthermore requires dedicated handling of special cases and degenerate constellations to achieve robustness on freeform surfaces. Another limitation is the small number of degrees of freedom for incorporating design parameters.
Using a variational re-formulation, we equip the concept of TPI with additional degrees of freedom and present a robust, unified approach for creating polygonal structures with planar faces that is readily able to integrate various objectives and constraints needed in different applications scenarios. We exemplarily demonstrate the abilities of our approach on three common problems in geometry processing.
Practical Mixed-Integer Optimization for Geometry Processing
Proceedings of Curves and Surfaces 2010
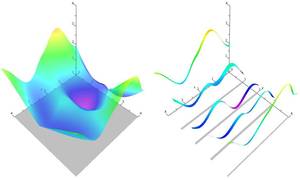
Solving mixed-integer problems, i.e., optimization problems where some of the unknowns are continuous while others are discrete, is NP-hard. Unfortunately, real-world problems like e.g., quadrangular remeshing usually have a large number of unknowns such that exact methods become unfeasible. In this article we present a greedy strategy to rapidly approximate the solution of large quadratic mixed-integer problems within a practically sufficient accuracy. The algorithm, which is freely available as an open source library implemented in C++, determines the values of the discrete variables by successively solving relaxed problems. Additionally the specification of arbitrary linear equality constraints which typically arise as side conditions of the optimization problem is possible. The performance of the base algorithm is strongly improved by two novel extensions which are (1) simultaneously estimating sets of discrete variables which do not interfere and (2) a fill-in reducing reordering of the constraints. Exemplarily the solver is applied to the problem of quadrilateral surface remeshing, enabling a great flexibility by supporting different types of user guidance within a real-time modeling framework for input surfaces of moderate complexity.
Mixed-Integer Quadrangulation
Proceedings of the 2009 SIGGRAPH Conference

We present a novel method for quadrangulating a given triangle mesh. After constructing an as smooth as possible symmetric cross field satisfying a sparse set of directional constraints (to capture the geometric structure of the surface), the mesh is cut open in order to enable a low distortion unfolding. Then a seamless globally smooth parametrization is computed whose iso-parameter lines follow the cross field directions. In contrast to previous methods, sparsely distributed directional constraints are sufficient to automatically determine the appropriate number, type and position of singularities in the quadrangulation. Both steps of the algorithm (cross field and parametrization) can be formulated as a mixed-integer problem which we solve very efficiently by an adaptive greedy solver. We show several complex examples where high quality quad meshes are generated in a fully automatic manner.
The Constrained Mixed-Integer Solver used in this project has been released under GPL and can be found on its projects page.

