Profile

|
Publications
GPU-Based Multiresolution Deformation Using Approximate Normal Field Reconstruction
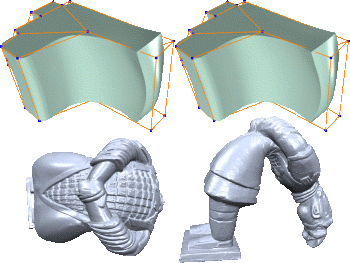
Multiresolution shape editing performs global deformations while preserving fine surface details by modifying a smooth base surface and reconstructing the modified detailed surface as a normal displacement from it. Since two non-trivial operators (deformation and reconstruction) are involved, the computational complexity can become too high for real-time deformations of complex models. We present an efficient technique for evaluating multiresolution deformations of high-resolution triangle meshes directly on the GPU. By precomputing the deformation functions as well as their gradient information we can map both the deformation and the reconstruction operator to the GPU, which enables us to reconstruct the deformed positions and sufficiently close approximations of the normal vectors in the vertex shader in a single rendering pass. This allows us to render dynamically deforming 3D models several times faster than on the CPU. We demonstrate the application of our technique to two modern multiresolution approaches: one based on (irregular) displaced subdivision surfaces and the other one on volumetric space deformation using radial basis functions.
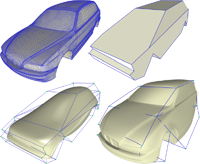
A Robust Two-Step Procedure for Quad-Dominant Remeshing
We propose a new technique for quad-dominant remeshing which separates the local regularity requirements from the global alignment requirements by working in two steps. In the first step, we apply a slight variant of variational shape approximation in order to segment the input mesh into patches which capture the global structure of the processed object. Then we compute an optimized quad-mesh for every patch by generating a finite set of candidate curves and applying a combinatorial optimization procedure. Since the optimization is performed independently for each patch, we can afford more complex operations while keeping the overall computation times at a reasonable level. Our quad-meshing technique is robust even for noisy meshes and meshes with isotropic or flat regions since it does not rely on the generation of curves by integration along estimated principal curvature directions. Instead we compute a conformal parametrization for each patch and generate the quad-mesh from curves with minimum bending energy in the 2D parameter domain. Mesh consistency between patches is guaranteed by simply using the same set of sample points along the common boundary curve. The resulting quad-meshes are of high-quality locally (shape of the quads) as well as globally (global alignment) which allows us to even generate fairly coarse quad-meshes that can be used as Catmull-Clark control meshes.
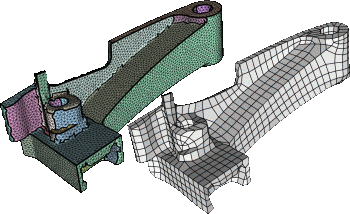
Automatic Generation of Structure Preserving Multiresolution Models
We are proposing a multiresolution representation which uses a subdivision surface as a smooth base surface with respect to which a high resolution mesh is defined by normal displacement. While this basic representation is quite straightforward, our actual contribution lies in the automatic generation of such a representation. Given a high resolution mesh, our algorithm is designed to derive a subdivision control mesh whose structure is properly adjusted and aligned to the major geometric features. This implies that the control vertices of the subdivision surface not only control globally smooth deformations but in addition that these deformations are meaningful in the sense that their support and shape correspond to the characteristic structure of the input mesh. This is achieved by using a new decimation scheme for general polygonal meshes (not just triangles) that is based on face merging instead of edge collapsing. A face-based integral metric makes the decimation scheme very robust such that we can obtain extremely coarse control meshes which in turn allow for deformations with large support.
Optimization Methods for Scattered Data Approximation with Subdivision Surfaces

We present a method for scattered data approximation with subdivision surfaces which actually uses the true representation of the limit surface as a linear combination of smooth basis functions associated with the control vertices. A robust and fast algorithm for exact closest point search on Loop surfaces which combines Newton iteration and non-linear minimization is used for parameterizing the samples. Based on this we perform unconditionally convergent parameter correction to optimize the approximation with respect to the L2 metric and thus we make a well-established scattered data fitting technique which has been available before only for B-spline surfaces, applicable to subdivision surfaces. We also adapt the recently discovered local second order squared distance function approximant to the parameter correction setup. Further we exploit the fact that the control mesh of a subdivision surface can have arbitrary connectivity to reduce the L? error up to a certain user-defined tolerance by adaptively restructuring the control mesh. Combining the presented algorithms we describe a complete procedure which is able to produce high-quality approximations of complex, detailed models.
Geometrically Controlled 4-Point Interpolatory Schemes

We present several non-linear 4-point interpolatory schemes, derived from the "classical" linear 4-point scheme. These new schemes have variable tension parameter instead of the fixed tension parameter in the linear 4-point scheme. The tension parameter is adapted locally according to the geometry of the control polygon within the 4-point stencil. This allows the schemes to remain local and in the same time to achieve two important shape-preserving properties - artifacts elimination and convexity-preservation. The proposed schemes are robust and have special features such as "double-knot" edges corresponding to continuity without geometrical smoothness and inflection edges support for convexity-preservation. Convergence proof is given and experimental smoothness analysis is done in detail, which indicates that the limit curves are C^1.
Optimization Techniques for Approximation with Subdivision Surfaces

We present a method for scattered data approximation with subdivision surfaces which actually uses the true representation of the limit surface as a linear combination of smooth basis functions associated with the control vertices. This is unlike previous techniques which used only piecewise linear approximations of the limit surface. By this we can assign arbitrary parameterizations to the given sample points, including those generated by parameter correction. We present a robust and fast algorithm for exact closest point search on Loop surfaces by combining Newton iteration and non-linear minimization. Based on this we perform unconditionally convergent parameter correction to optimize the approximation with respect to the L^2 metric and thus we make a well-established scattered data fitting technique which has been available before only for B-spline surfaces, applicable to subdivision surfaces. Further we exploit the fact that the control mesh of a subdivision surface can have arbitrary connectivity to reduce the L^\infty error up to a certain user-defined tolerance by adaptively restructuring the control mesh. By employing iterative least squares solvers, we achieve acceptable running times even for large amounts of data and we obtain high quality approximations by surfaces with relatively low control mesh complexity compared to the number of sample points. Since we are using plain subdivision surfaces, there is no need for multiresolution detail coefficients and we do not have to deal with the additional overhead in data and computational complexity associated with them.
Direct Anisotropic Quad-Dominant Remeshing

We present an extension of the anisotropic polygonal remeshing technique developed by Alliez et al. Our algorithm does not rely on a global parameterization of the mesh and therefore is applicable to arbitrary genus surfaces. We show how to exploit the structure of the original mesh in order to perform efficiently the proximity queries required in the line integration phase, thus improving dramatically the scalability and the performance of the original algorithm. Finally, we propose a novel technique for producing conforming quad-dominant meshes in isotropic regions as well by propagating directional information from the anisotropic regions.

