Publications

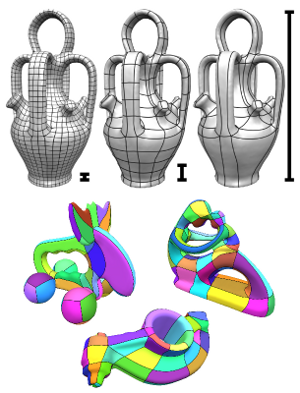
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths, state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts – a difficult task solely tackled by greedy methodologies before.

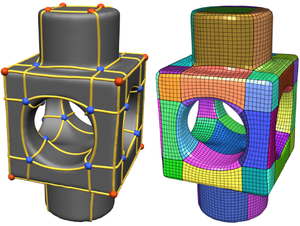
We present a theoretical framework and practical method for the automatic construction of simple, all-quadrilateral patch layouts on manifold surfaces. The resulting layouts are coarse, surface-embedded cell complexes well adapted to the geometric structure, hence they are ideally suited as domains and base complexes for surface parameterization, spline fitting, or subdivision surfaces and can be used to generate quad meshes with a high-level patch structure that are advantageous in many application scenarios. Our approach is based on the careful construction of the layout graph's combinatorial dual. In contrast to the primal this dual perspective provides direct control over the globally interdependent structural constraints inherent to quad layouts. The dual layout is built from curvature-guided, crossing loops on the surface. A novel method to construct these efficiently in a geometry- and structure-aware manner constitutes the core of our approach.

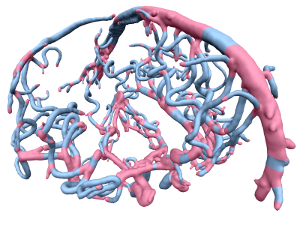
We present a pipeline to generate high quality quad dominant meshes for vascular structures from a given volumetric image. As common for medical image segmentation we use a Level Set approach to separate the region of interest from the background. However in contrast to the standard method we control the topology of the deformable object – defined by the Level Set function – which allows us to extract a proper skeleton which represents the global topological information of the vascular structure. Instead of solving a complex global optimization problem to compute a quad mesh, we divide the problem and partition the complex model into junction and tube elements, employing the skeleton of the vascular structure. After computing quad meshes for the junctions using the Mixed Integer Quadrangulation approach, we re-mesh the tubes using an algorithm inspired by the well known Bresenham Algorithm for drawing lines which distributes irregular elements equally over the entire tube element.

We introduce a fully automatic algorithm which optimizes the high-level structure of a given quadrilateral mesh to achieve a coarser quadrangular base complex. Such a topological optimization is highly desirable, since state-of-the-art quadrangulation techniques lead to meshes which have an appropriate singularity distribution and an anisotropic element alignment, but usually they are still far away from the high-level structure which is typical for carefully designed meshes manually created by specialists and used e.g. in animation or simulation. In this paper we show that the quality of the high-level structure is negatively affected by helical configurations within the quadrilateral mesh. Consequently we present an algorithm which detects helices and is able to remove most of them by applying a novel grid preserving simplification operator (GP-operator) which is guaranteed to maintain an all-quadrilateral mesh. Additionally it preserves the given singularity distribution and in particular does not introduce new singularities. For each helix we construct a directed graph in which cycles through the start vertex encode operations to remove the corresponding helix. Therefore a simple graph search algorithm can be performed iteratively to remove as many helices as possible and thus improve the high-level structure in a greedy fashion. We demonstrate the usefulness of our automatic structure optimization technique by showing several examples with varying complexity.

We present a novel method for quadrangulating a given triangle mesh. After constructing an as smooth as possible symmetric cross field satisfying a sparse set of directional constraints (to capture the geometric structure of the surface), the mesh is cut open in order to enable a low distortion unfolding. Then a seamless globally smooth parametrization is computed whose iso-parameter lines follow the cross field directions. In contrast to previous methods, sparsely distributed directional constraints are sufficient to automatically determine the appropriate number, type and position of singularities in the quadrangulation. Both steps of the algorithm (cross field and parametrization) can be formulated as a mixed-integer problem which we solve very efficiently by an adaptive greedy solver. We show several complex examples where high quality quad meshes are generated in a fully automatic manner.

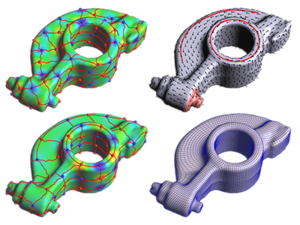
This paper presents a new quadrangulation algorithm, extending the spectral surface quadrangulation approach where the coarse quadrangular structure is derived from the Morse-Smale complex of an eigenfunction of the Laplacian operator on the input mesh. In contrast to the original scheme, we provide flexible explicit controls of the shape, size, orientation and feature alignment of the quadrangular faces. We achieve this by proper selection of the optimal eigenvalue (shape), by adaption of the area term in the Laplacian operator (size), and by adding special constraints to the Laplace eigenproblem (orientation and alignment). By solving a generalized eigenproblem we can generate a scalar field on the mesh whose Morse-Smale complex is of high quality and satisfies all the user requirements. The final quadrilateral mesh is generated from the Morse- Smale complex by computing a globally smooth parametrization. Here we additionally introduce edge constraints to preserve user specified feature lines accurately.

In this paper we present a new algorithm which turns an unstructured triangle mesh into a quad-dominant mesh with edges aligned to the principal directions of the underlying geometry. Instead of computing a globally smooth parameterization or integrating curvature lines along a tangent vector field, we simply apply an iterative relaxation scheme which incrementally aligns the mesh edges to the principal directions. The quad-dominant mesh is eventually obtained by dropping the not-aligned diagonals from the triangle mesh. A post-processing stage is introduced to further improve the results. The major advantage of our algorithm is its conceptual simplicity since it is merely based on elementary mesh operations such as edge collapse, flip, and split. The resulting meshes exhibit a very good alignment to surface features and rather uniform distribution of mesh vertices. This makes them very well-suited, e.g., as Catmull-Clark Subdivision control meshes.

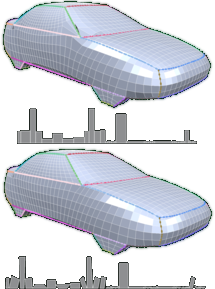
The aim of Reverse Engineering is to convert an unstructured representation of a geometric object, emerging e.g. from laser scanners, into a natural, structured representation in the spirit of CAD models, which is suitable for numerical computations. Therefore we present a user-controlled, as isometric as possible parameterization technique which is able to prescribe geometric features of the input and produces high-quality quadmeshes with low distortion. Starting with a coarse, user-prescribed layout this is achieved by using affine functions for the transition between non-orthogonal quadrangular charts of a global parameterization. The shape of each chart is optimized non-linearly for isometry of the underlying parameterization to produce meshes with low edge-length distortion. To provide full control over the meshing alignment the user can additionally tag an arbitrary subset of the layout edges which are guaranteed to be represented by enforcing them to lie on iso-lines of the parameterization but still allowing the global parameterization to relax in the direction of the iso-lines.

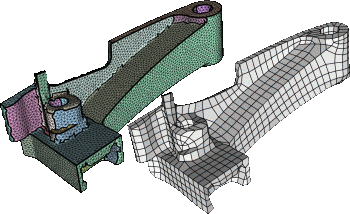
We propose a new technique for quad-dominant remeshing which separates the local regularity requirements from the global alignment requirements by working in two steps. In the first step, we apply a slight variant of variational shape approximation in order to segment the input mesh into patches which capture the global structure of the processed object. Then we compute an optimized quad-mesh for every patch by generating a finite set of candidate curves and applying a combinatorial optimization procedure. Since the optimization is performed independently for each patch, we can afford more complex operations while keeping the overall computation times at a reasonable level. Our quad-meshing technique is robust even for noisy meshes and meshes with isotropic or flat regions since it does not rely on the generation of curves by integration along estimated principal curvature directions. Instead we compute a conformal parametrization for each patch and generate the quad-mesh from curves with minimum bending energy in the 2D parameter domain. Mesh consistency between patches is guaranteed by simply using the same set of sample points along the common boundary curve. The resulting quad-meshes are of high-quality locally (shape of the quads) as well as globally (global alignment) which allows us to even generate fairly coarse quad-meshes that can be used as Catmull-Clark control meshes.

We present an extension of the anisotropic polygonal remeshing technique developed by Alliez et al. Our algorithm does not rely on a global parameterization of the mesh and therefore is applicable to arbitrary genus surfaces. We show how to exploit the structure of the original mesh in order to perform efficiently the proximity queries required in the line integration phase, thus improving dramatically the scalability and the performance of the original algorithm. Finally, we propose a novel technique for producing conforming quad-dominant meshes in isotropic regions as well by propagating directional information from the anisotropic regions.