Profile

|
Presentations
Event |
Type |
Title |
|---|---|---|
| SIGGRAPH 2017 | Paper | Similarity Maps and Field-Guided T-Splines: a Perfect Couple |
| SIGGRAPH 2017 | Course | Directional Field Synthesis, Design, and Processing |
| SGP 2017 | Course | Quad Mesh Generation |
| Eurographics 2017 | Tutorial | Partitioning Surfaces into Quad Patches |
| SIGGRAPH Asia 2016 | Course | Directional Field Synthesis, Design, and Processing |
| SIGGRAPH 2016 | Paper | Bijective Maps from Simplicial Foliations |
| SGP 2016 | Course | Quad Mesh Generation |
| SGP 2016 | Paper | Scale-Invariant Directional Alignment of Surface Parametrizations |
| Eurographics 2016 | Paper | Directional Field Synthesis, Design, and Processing |
| SIGGRAPH Asia 2015 | Paper | Quantized Global Parametrization |
| Eurographics 2015 | Paper | Quad Layout Embedding via Aligned Parameterization |
| LGG, EPFL | Invited Talk | From Quad Meshes to Quad Layouts |
| SIGGRAPH Asia 2014 | Paper | Dual Strip Weaving: Interactive Design of Quad Layouts using Elastica Strips |
| Titane Seminar, INRIA Sophia Antipolis | Invited Talk | Quad Layouts on Surfaces: Generation and Optimization |
| SGP 2013 | Paper | Practical Anisotropic Geodesy |
| SGP 2013 | Course | Fixing Mesh Defects - Algorithms and Techniques |
| SIGGRAPH 2012 | Paper | Dual Loops Meshing: Quality Quad Layouts on Manifolds |
| Eurographics 2012 | Tutorial | Polygon Mesh Repairing |
| Eurographics 2011 | Paper | Hybrid Booleans |
| Eurographics 2011 | Paper | Walking On Broken Mesh: Defect-Tolerant Geodesic Distances and Parameterizations |
| SGP 2010 | Paper | Polygonal Boundary Evaluation of Minkowski Sums and Swept Volumes |
| Eurographics 2010 | Paper | Exact and Robust (Self-)Intersections for Polygonal Meshes |
| New Trends in Applied Geometry 2010 | Talk | Hybrid Geometry Processing: Booleans, Offsets, Repairing |
| GI Informatik-Tage 2009 | Poster | A Framework for Geometry Processing based on Hybrid Surface Representations |
Publications
TinyAD: Automatic Differentiation in Geometry Processing Made Simple

Non-linear optimization is essential to many areas of geometry processing research. However, when experimenting with different problem formulations or when prototyping new algorithms, a major practical obstacle is the need to figure out derivatives of objective functions, especially when second-order derivatives are required. Deriving and manually implementing gradients and Hessians is both time-consuming and error-prone. Automatic differentiation techniques address this problem, but can introduce a diverse set of obstacles themselves, e.g. limiting the set of supported language features, imposing restrictions on a program's control flow, incurring a significant run time overhead, or making it hard to exploit sparsity patterns common in geometry processing. We show that for many geometric problems, in particular on meshes, the simplest form of forward-mode automatic differentiation is not only the most flexible, but also actually the most efficient choice. We introduce TinyAD: a lightweight C++ library that automatically computes gradients and Hessians, in particular of sparse problems, by differentiating small (tiny) sub-problems. Its simplicity enables easy integration; no restrictions on, e.g., looping and branching are imposed. TinyAD provides the basic ingredients to quickly implement first and second order Newton-style solvers, allowing for flexible adjustment of both problem formulations and solver details. By showcasing compact implementations of methods from parametrization, deformation, and direction field design, we demonstrate how TinyAD lowers the barrier to exploring non-linear optimization techniques. This enables not only fast prototyping of new research ideas, but also improves replicability of existing algorithms in geometry processing. TinyAD is available to the community as an open source library.
- Best Paper Award (1st place) at SGP 2022
- Graphics Replicability Stamp
» Show BibTeX
@article{schmidt2022tinyad,
title={{TinyAD}: Automatic Differentiation in Geometry Processing Made Simple},
author={Schmidt, Patrick and Born, Janis and Bommes, David and Campen, Marcel and Kobbelt, Leif},
year={2022},
journal={Computer Graphics Forum},
volume={41},
number={5},
}
Simpler Quad Layouts using Relaxed Singularities
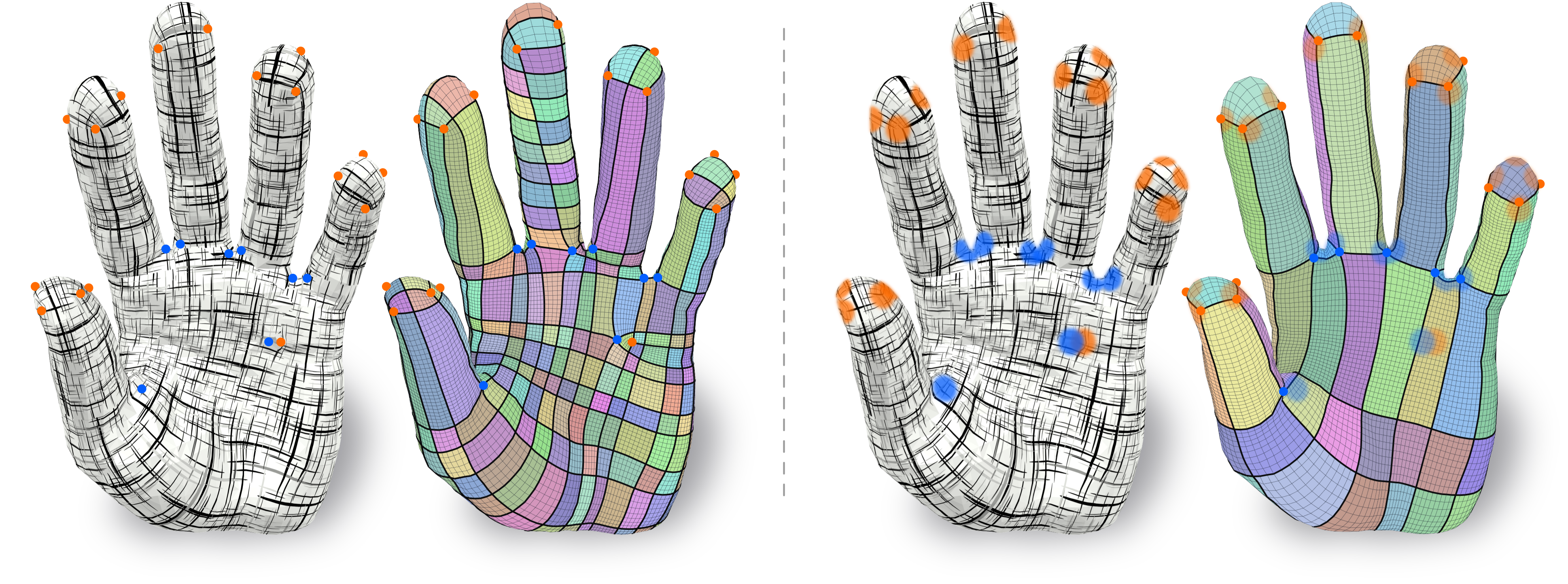
A common approach to automatic quad layout generation on surfaces is to, in a first stage, decide on the positioning of irregular layout vertices, followed by finding sensible layout edges connecting these vertices and partitioning the surface into quadrilateral patches in a second stage. While this two-step approach reduces the problem's complexity, this separation also limits the result quality. In the worst case, the set of layout vertices fixed in the first stage without consideration of the second may not even permit a valid quad layout. We propose an algorithm for the creation of quad layouts in which the initial layout vertices can be adjusted in the second stage. Whenever beneficial for layout quality or even validity, these vertices may be moved within a prescribed radius or even be removed. Our algorithm is based on a robust quantization strategy, turning a continuous T-mesh structure into a discrete layout. We show the effectiveness of our algorithm on a variety of inputs.
» Show BibTeX
@article{lyon2021simplerlayouts,
title={Simpler Quad Layouts using Relaxed Singularities},
author={Lyon, Max and Campen, Marcel and Kobbelt, Leif},
year={2021},
journal={Computer Graphics Forum},
volume={40},
number={5},
}
Surface Map Homology Inference

A homeomorphism between two surfaces not only defines a (continuous and bijective) geometric correspondence of points but also (by implication) an identification of topological features, i.e. handles and tunnels, and how the map twists around them. However, in practice, surface maps are often encoded via sparse correspondences or fuzzy representations that merely approximate a homeomorphism and are therefore inherently ambiguous about map topology. In this work, we show a way to infer topological information from an imperfect input map between two shapes. In particular, we compute a homology map, a linear map that transports homology classes of cycles from one surface to the other, subject to a global consistency constraint. Our inference robustly handles imperfect (e.g., partial, sparse, fuzzy, noisy, outlier-ridden, non-injective) input maps and is guaranteed to produce homology maps that are compatible with true homeomorphisms between the input shapes. Homology maps inferred by our method can be directly used to transfer homological information between shapes, or serve as foundation for the construction of a proper homeomorphism guided by the input map, e.g., via compatible surface decomposition.
- Best Paper Award at SGP 2021
- Graphics Replicability Stamp
» Show BibTeX
@article{born2021surface,
title={Surface Map Homology Inference},
author={Born, Janis and Schmidt, Patrick and Campen, Marcel and Kobbelt, Leif},
year={2021},
journal={Computer Graphics Forum},
volume={40},
number={5},
}
Quad Layouts via Constrained T-Mesh Quantization

We present a robust and fast method for the creation of conforming quad layouts on surfaces. Our algorithm is based on the quantization of a T-mesh, i.e. an assignment of integer lengths to the sides of a non-conforming rectangular partition of the surface. This representation has the benefit of being able to encode an infinite number of layout connectivity options in a finite manner, which guarantees that a valid layout can always be found. We carefully construct the T-mesh from a given seamless parametrization such that the algorithm can provide guarantees on the results' quality. In particular, the user can specify a bound on the angular deviation of layout edges from prescribed directions. We solve an integer linear program (ILP) to find a coarse quad layout adhering to that maximal deviation. Our algorithm is guaranteed to yield a conforming quad layout free of T-junctions together with bounded angle distortion. Our results show that the presented method is fast, reliable, and achieves high quality layouts.
» Show BibTeX
@article{Lyon:2021:Quad,
title = {Quad Layouts via Constrained T-Mesh Quantization},
author = {Lyon, Max and Campen, Marcel and Kobbelt, Leif},
journal = {Computer Graphics Forum},
volume = {40},
number = {2},
year = {2021}
}
Inter-Surface Maps via Constant-Curvature Metrics
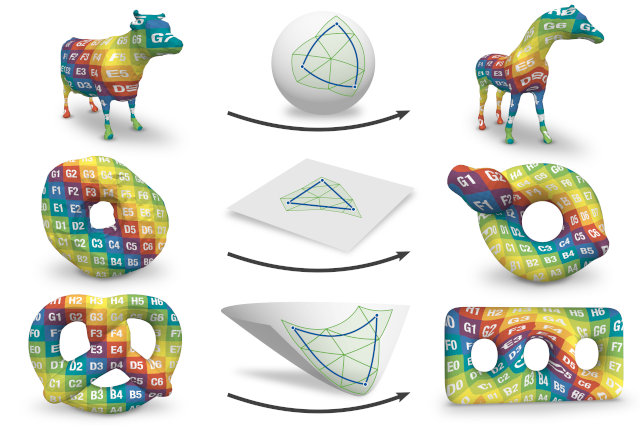
We propose a novel approach to represent maps between two discrete surfaces of the same genus and to minimize intrinsic mapping distortion. Our maps are well-defined at every surface point and are guaranteed to be continuous bijections (surface homeomorphisms). As a key feature of our approach, only the images of vertices need to be represented explicitly, since the images of all other points (on edges or in faces) are properly defined implicitly. This definition is via unique geodesics in metrics of constant Gaussian curvature. Our method is built upon the fact that such metrics exist on surfaces of arbitrary topology, without the need for any cuts or cones (as asserted by the uniformization theorem). Depending on the surfaces' genus, these metrics exhibit one of the three classical geometries: Euclidean, spherical or hyperbolic. Our formulation handles constructions in all three geometries in a unified way. In addition, by considering not only the vertex images but also the discrete metric as degrees of freedom, our formulation enables us to simultaneously optimize the images of these vertices and images of all other points.
» Show BibTeX
@article{schmidt2020intersurface,
author = {Schmidt, Patrick and Campen, Marcel and Born, Janis and Kobbelt, Leif},
title = {Inter-Surface Maps via Constant-Curvature Metrics},
journal = {ACM Transactions on Graphics},
issue_date = {July 2020},
volume = {39},
number = {4},
month = jul,
year = {2020},
articleno = {119},
url = {https://doi.org/10.1145/3386569.3392399},
doi = {10.1145/3386569.3392399},
publisher = {ACM},
address = {New York, NY, USA},
}
Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing

The generation of quad meshes based on surface parametrization techniques has proven to be a versatile approach. These techniques quantize an initial seamless parametrization so as to obtain an integer grid map implying a pure quad mesh. State-of-the-art methods following this approach have to assume that the surface to be meshed either has no boundary, or has a boundary which the resulting mesh is supposed to be aligned to. In a variety of applications this is not desirable and non-boundary-aligned meshes or grid-parametrizations are preferred. We thus present a technique to robustly generate integer grid maps which are either boundary-aligned, non-boundary-aligned, or partially boundary-aligned, just as required by different applications. We thereby generalize previous work to this broader setting. This enables the reliable generation of trimmed quad meshes with partial elements along the boundary, preferable in various scenarios, from tiled texturing over design and modeling to fabrication and architecture, due to fewer constraints and hence higher overall mesh quality and other benefits in terms of aesthetics and flexibility.
@article{Lyon:2019:TrimmedQuadMeshing,
author = "Lyon, Max and Campen, Marcel and Bommes, David and Kobbelt, Leif",
title = "Parametrization Quantization with Free Boundaries for Trimmed Quad Meshing",
journal = "ACM Transactions on Graphics",
volume = 38,
number = 4,
year = 2019
}
Distortion-Minimizing Injective Maps Between Surfaces
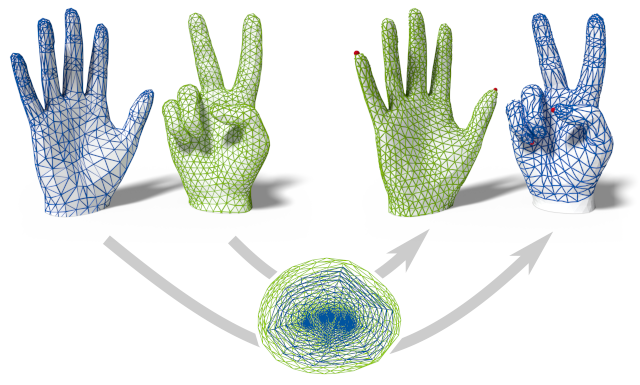
The problem of discrete surface parametrization, i.e. mapping a mesh to a planar domain, has been investigated extensively. We address the more general problem of mapping between surfaces. In particular, we provide a formulation that yields a map between two disk-topology meshes, which is continuous and injective by construction and which locally minimizes intrinsic distortion. A common approach is to express such a map as the composition of two maps via a simple intermediate domain such as the plane, and to independently optimize the individual maps. However, even if both individual maps are of minimal distortion, there is potentially high distortion in the composed map. In contrast to many previous works, we minimize distortion in an end-to-end manner, directly optimizing the quality of the composed map. This setting poses additional challenges due to the discrete nature of both the source and the target domain. We propose a formulation that, despite the combinatorial aspects of the problem, allows for a purely continuous optimization. Further, our approach addresses the non-smooth nature of discrete distortion measures in this context which hinders straightforward application of off-the-shelf optimization techniques. We demonstrate that, despite the challenges inherent to the more involved setting, discrete surface-to-surface maps can be optimized effectively.
» Show BibTeX
@article{schmidt2019distortion,
author = {Schmidt, Patrick and Born, Janis and Campen, Marcel and Kobbelt, Leif},
title = {Distortion-Minimizing Injective Maps Between Surfaces},
journal = {ACM Transactions on Graphics},
issue_date = {November 2019},
volume = {38},
number = {6},
month = nov,
year = {2019},
articleno = {156},
url = {https://doi.org/10.1145/3355089.3356519},
doi = {10.1145/3355089.3356519},
publisher = {ACM},
address = {New York, NY, USA},
}
A Simple Approach to Intrinsic Correspondence Learning on Unstructured 3D Meshes
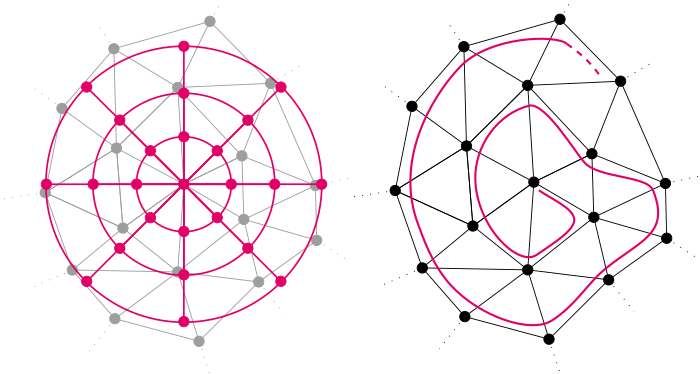
The question of representation of 3D geometry is of vital importance when it comes to leveraging the recent advances in the field of machine learning for geometry processing tasks. For common unstructured surface meshes state-of-the-art methods rely on patch-based or mapping-based techniques that introduce resampling operations in order to encode neighborhood information in a structured and regular manner. We investigate whether such resampling can be avoided, and propose a simple and direct encoding approach. It does not only increase processing efficiency due to its simplicity - its direct nature also avoids any loss in data fidelity. To evaluate the proposed method, we perform a number of experiments in the challenging domain of intrinsic, non-rigid shape correspondence estimation. In comparisons to current methods we observe that our approach is able to achieve highly competitive results.
@InProceedings{lim2018_correspondence_learning,
author = {Lim, Isaak and Dielen, Alexander and Campen, Marcel and Kobbelt, Leif},
title = {A Simple Approach to Intrinsic Correspondence Learning on Unstructured 3D Meshes},
booktitle = {The European Conference on Computer Vision (ECCV) Workshops},
month = {September},
year = {2018}
}
Directional Field Synthesis, Design, and Processing

Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This course provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.
@inproceedings{Vaxman:2017:DFS:3084873.3084921,
author = {Vaxman, Amir and Campen, Marcel and Diamanti, Olga and Bommes, David and Hildebrandt, Klaus and Technion, Mirela Ben-Chen and Panozzo, Daniele},
title = {Directional Field Synthesis, Design, and Processing},
booktitle = {ACM SIGGRAPH 2017 Courses},
series = {SIGGRAPH '17},
year = {2017},
isbn = {978-1-4503-5014-3},
location = {Los Angeles, California},
pages = {12:1--12:30},
articleno = {12},
numpages = {30},
url = {http://doi.acm.org/10.1145/3084873.3084921},
doi = {10.1145/3084873.3084921},
acmid = {3084921},
publisher = {ACM},
address = {New York, NY, USA},
}
Similarity Maps and Field-Guided T-Splines: a Perfect Couple

A variety of techniques were proposed to model smooth surfaces based on tensor product splines (e.g. subdivision surfaces, free-form splines, T-splines). Conversion of an input surface into such a representation is commonly achieved by constructing a global seamless parametrization, possibly aligned to a guiding cross-field (e.g. of principal curvature directions), and using this parametrization as domain to construct the spline-based surface. One major fundamental difficulty in designing robust algorithms for this task is the fact that for common types, e.g. subdivision surfaces (requiring a conforming domain mesh) or T-spline surfaces (requiring a globally consistent knot interval assignment) reliably obtaining a suitable parametrization that has the same topological structure as the guiding field poses a major challenge. Even worse, not all fields do admit suitable parametrizations, and no concise conditions are known as to which fields do. We present a class of surface constructions (T-splines with halfedge knots) and a class of parametrizations (seamless similarity maps) that are, in a sense, a perfect match for the task: for any given guiding field structure, a compatible parametrization of this kind exists and a smooth piecewise rational surface with exactly the same structure as the input field can be constructed from it. As a byproduct, this enables full control over extraordinary points. The construction is backward compatible with classical NURBS. We present efficient algorithms for building discrete conformal similarity maps and associated T-meshes and T-spline surfaces.
@article{Campen:2017:Similarity,
author = "Campen, Marcel and Zorin, Denis",
title = "Similarity Maps and Field-Guided T-Splines: a Perfect Couple",
journal = "ACM Transactions on Graphics",
volume = 36,
number = 4,
year = 2017
}
Partitioning Surfaces into Quadrilateral Patches: A Survey
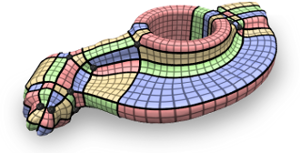
The efficient and practical representation and processing of geometrically or topologically complex shapes often demands a partitioning into simpler patches. Possibilities range from unstructured arrangements of arbitrarily shaped patches on the one end, to highly structured conforming networks of all-quadrilateral patches on the other end of the spectrum. Due to its regularity, this latter extreme of conforming partitions with quadrilateral patches, called quad layouts, is most beneficial in many application scenarios, for instance enabling the use of tensor-product representations based on NURBS or Bézier patches, grid-based multiresolution techniques, and discrete pixel-based map representations. However, this type of partition is also most complicated to create due to the strict inherent structural restrictions. Traditionally often performed manually in a tedious and demanding process, research in computer graphics and geometry processing has led to a number of computer-assisted, semi- automatic, as well as fully automatic approaches to address this problem more efficiently. This survey provides a detailed discussion of this range of methods, treats their strengths and weaknesses, and outlines open problems in this field of research.
Tiling the Bunny: Quad Layouts for Efficient 3D Geometry Representation

Ultimately, any information to be processed by computers must be represented as a plain sequence of numbers. This poses a major challenge when representing complex 3D shapes. Marcel Campen's research explores how to efficiently identify a good quad layout, a partition of a surface into simple four-sided pieces.
Bijective Maps from Simplicial Foliations
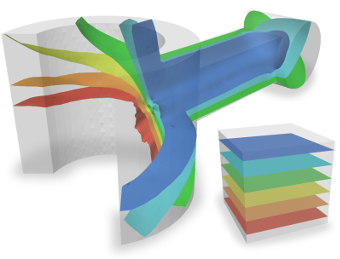
This paper presents a method for bijective parametrization of 2D and 3D objects over canonical domains. While a range of solutions for the two-dimensional case are well-known, our method guarantees bijectivity of mappings also for a large, combinatorially-defined class of tetrahedral meshes (shellable meshes). The key concept in our method is the piecewise-linear (PL) foliation, decomposing the mesh into one-dimensional submanifolds and reducing the mapping problem to parametrization of a lower-dimensional manifold (a foliation section). The maps resulting from these foliations are proved to be bijective and continuous, and shown to have provably bijective PL approximations. We describe exact, numerically robust evaluation methods and demonstrate our implementation's capabilities on a large variety of meshes.
@article{Campen:2016:Bijective,
author = "Campen, Marcel and Silva, Claudio T. and Zorin, Denis",
title = "Bijective Maps from Simplicial Foliations",
journal = "ACM Transactions on Graphics",
volume = 35,
number = 4,
year = 2016
}
Interactively Controlled Quad Remeshing of High Resolution 3D Models

Parametrization based methods have recently become very popular for the generation of high quality quad meshes. In contrast to previous approaches, they allow for intuitive user control in order to accommodate all kinds of application driven constraints and design intentions. A major obstacle in practice, however, are the relatively long computations that lead to response times of several minutes already for input models of moderate complexity. In this paper we introduce a novel strategy to handle highly complex input meshes with up to several millions of triangles such that quad meshes can still be created and edited within an interactive workflow. Our method is based on representing the input model on different levels of resolution with a mechanism to propagate parametrizations from coarser to finer levels. The major challenge is to guarantee consistent parametrizations even in the presence of charts, transition functions, and singularities. Moreover, the remaining degrees of freedom on coarser levels of resolution have to be chosen carefully in order to still achieve low distortion parametrizations. We demonstrate a prototypic system where the user can interactively edit quad meshes with powerful high-level operations such as guiding constraints, singularity repositioning, and singularity connections.
» Show BibTeX
@article{esck2016,
author = {Ebke, Hans-Christian and Schmidt, Patrick and Campen, Marcel and Kobbelt, Leif},
title = {Interactively Controlled Quad Remeshing of High Resolution 3D Models},
journal = {ACM Trans. Graph.},
issue_date = {November 2016},
volume = {35},
number = {6},
month = nov,
year = {2016},
issn = {0730-0301},
pages = {218:1--218:13},
articleno = {218},
url = {http://doi.acm.org/10.1145/2980179.2982413},
doi = {10.1145/2980179.2982413},
acmid = {2982413},
publisher = {ACM},
address = {New York, NY, USA},
}
Directional Field Synthesis, Design, and Processing
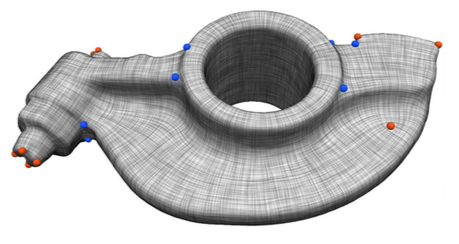
Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This report provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.
Scale-Invariant Directional Alignment of Surface Parametrizations

Various applications of global surface parametrization benefit from the alignment of parametrization isolines with principal curvature directions. This is particularly true for recent parametrization-based meshing approaches, where this directly translates into a shape-aware edge flow, better approximation quality, and reduced meshing artifacts. Existing methods to influence a parametrization based on principal curvature directions suffer from scale-dependence, which implies the necessity of parameter variation, or try to capture complex directional shape features using simple 1D curves. Especially for non-sharp features, such as chamfers, fillets, blends, and even more for organic variants thereof, these abstractions can be unfit. We present a novel approach which respects and exploits the 2D nature of such directional feature regions, detects them based on coherence and homogeneity properties, and controls the parametrization process accordingly. This approach enables us to provide an intuitive, scale-invariant control parameter to the user. It also allows us to consider non-local aspects like the topology of a feature, enabling further improvements. We demonstrate that, compared to previous approaches, global parametrizations of higher quality can be generated without user intervention.
@article{Campen:2016:ScaleInvariant,
author = "Campen, Marcel and Ibing, Moritz and Ebke, Hans-Christian and Zorin, Denis and Kobbelt, Leif",
title = "Scale-Invariant Directional Alignment of Surface Parametrizations",
journal = "Computer Graphics Forum",
volume = 35,
number = 5,
year = 2016
}
Quantized Global Parametrization
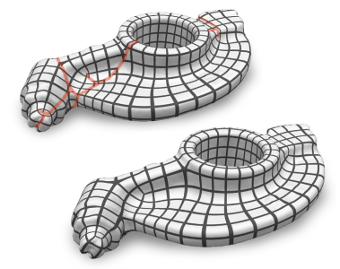
Global surface parametrization often requires the use of cuts or charts due to non-trivial topology. In recent years a focus has been on so-called seamless parametrizations, where the transition functions across the cuts are rigid transformations with a rotation about some multiple of 90 degrees. Of particular interest, e.g. for quadrilateral meshing, paneling, or texturing, are those instances where in addition the translational part of these transitions is integral (or more generally: quantized). We show that finding not even the optimal, but just an arbitrary valid quantization (one that does not imply parametric degeneracies), is a complex combinatorial problem. We present a novel method that allows us to solve it, i.e. to find valid as well as good quality quantizations. It is based on an original approach to quickly construct solutions to linear Diophantine equation systems, exploiting the specific geometric nature of the parametrization problem. We thereby largely outperform the state-of-the-art, sometimes by several orders of magnitude.
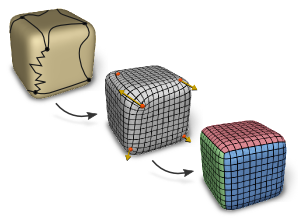
Level-of-Detail Quad Meshing
The most effective and popular tools for obtaining feature aligned quad meshes from triangular input meshes are based on cross field guided parametrization. These methods are incarnations of a conceptual three-step pipeline: (1) cross field computation, (2) field-guided surface parametrization, (3) quad mesh extraction. While in most meshing scenarios the user prescribes a desired target quad size or edge length, this information is typically taken into account from step 2 onwards only, but not in the cross field computation step. This turns into a problem in the presence of small scale geometric or topological features or noise in the input mesh: closely placed singularities are induced in the cross field, which are not properly reproducible by vertices in a quad mesh with the prescribed edge length, causing severe distortions or even failure of the meshing algorithm. We reformulate the construction of cross fields as well as field-guided parametrizations in a scale-aware manner which effectively suppresses densely spaced features and noise of geometric as well as topological kind. Dominant large-scale features are adequately preserved in the output by relying on the unaltered input mesh as the computational domain.
Dual Strip Weaving: Interactive Design of Quad Layouts using Elastica Strips

We introduce Dual Strip Weaving, a novel concept for the interactive design of quad layouts, i.e. partitionings of freeform surfaces into quadrilateral patch networks. In contrast to established tools for the design of quad layouts or subdivision base meshes, which are often based on creating individual vertices, edges, and quads, our method takes a more global perspective, operating on a higher level of abstraction: the atomic operation of our method is the creation of an entire cyclic strip, delineating a large number of quad patches at once. The global consistency-preserving nature of this approach reduces demands on the user’s expertise by requiring less advance planning. Efficiency is achieved using a novel method at the heart of our system, which automatically proposes geometrically and topologically suitable strips to the user. Based on this we provide interaction tools to influence the design process to any desired degree and visual guides to support the user in this task.
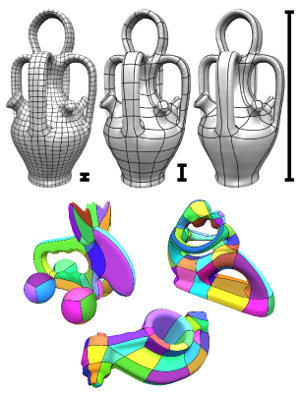
Quad Layout Embedding via Aligned Parameterization
Quad layouting, i.e. the partitioning of a surface into a coarse network of quadrilateral patches, is a fundamental step in application scenarios ranging from animation and simulation to reverse engineering and meshing. This process involves determining the layout's combinatorial structure as well as its geometric embedding in the surface. We present a novel quad layout algorithm that focuses on the embedding optimization, thereby complementing recent methods focusing on the structure optimization aspect. It takes as input a description of the target layout structure and computes a complete embedding in form of a parameterization globally optimized for isometry and, in particular, principal direction alignment. Besides being suited for fully automatic workflows, our method can also incorporate user constraints and support the tedious but common procedure of manual layouting.
Quad Layouts – Generation and Optimization of Conforming Quadrilateral Surface Partitions
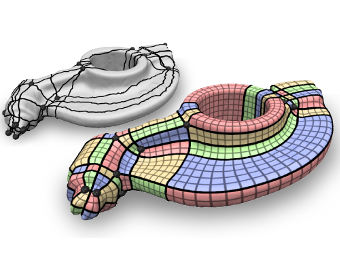
The efficient, computer aided or automatic generation of quad layouts, i.e. the partitioning of an object’s surface into simple networks of conforming quadrilateral patches, is a task that – despite its importance and utility in Computer Graphics and Geometric Modeling – received relatively low attention in the past. As a consequence, this task is most often performed manually by well-trained experts in practice, where quad layouts are of particular interest for surface representation and parameterization tasks. Deeper analysis reveals the inherent complexity of this problem, which might be one of the underlying reasons for this situation. In this thesis we investigate the structure of the problem and the commonly relevant quality criteria. Based on this we develop novel efficient solution strategies and algorithms for the generation of high quality quad layouts. In particular, we present a fully automatic as well as an interactive pipeline for this task. Both are based on splitting the hard problem into sub-problems with a simpler structure each. For each sub-problem we design efficient, custom-tailored optimization algorithms motivated by the geometric nature of these problems. In this process we pay attention to compatibility, such that these algorithms can be applied in sequence, forming the stages of efficient quad layouting pipelines.
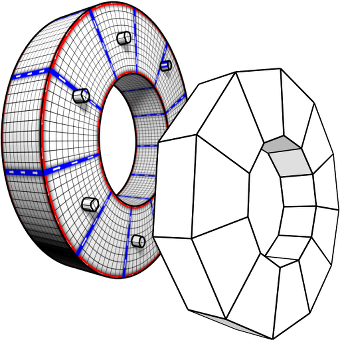
Integer-Grid Maps for Reliable Quad Meshing
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths, state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts – a difficult task solely tackled by greedy methodologies before.
QEx: Robust Quad Mesh Extraction

The most popular and actively researched class of quad remeshing techniques is
the family of parametrization based quad meshing methods. They all strive
to generate an integer-grid map, i.e. a parametrization of the input surface
into R2 such that the canonical grid of integer iso-lines forms a
quad mesh when mapped back onto the surface in R3. An essential,
albeit broadly neglected aspect of these methods is the quad extraction
step, i.e. the materialization of an actual quad mesh from the mere “quad
texture”. Quad (mesh) extraction is often believed to be a trivial matter but
quite the opposite is true: Numerous special cases, ambiguities induced by
numerical inaccuracies and limited solver precision, as well as imperfections
in the maps produced by most methods (unless costly countermeasures are taken)
pose significant challenges to the quad extractor. We present a method to
sanitize a provided parametrization such that it becomes numerically
consistent even in a limited precision floating point representation. Based
on this we are able to provide a comprehensive and sound description of how to
perform quad extraction robustly and without the need for any complex
tolerance thresholds or disambiguation rules. On top of that we develop a
novel strategy to cope with common local fold-overs in the parametrization.
This allows our method, dubbed QEx, to generate all-quadrilateral meshes
where otherwise holes, non-quad polygons or no output at all would have been
produced. We thus enable the practical use of an entire class of maps that was
previously considered defective. Since state of the art quad meshing methods
spend a significant share of their run time solely to prevent local
fold-overs, using our method it is now possible to obtain quad meshes
significantly quicker than before. We also provide libQEx, an open source
C++ reference implementation of our method and thus significantly lower the
bar to enter the field of quad meshing.
Efficient Computation of Shortest Path-Concavity for 3D Meshes

In the context of shape segmentation and retrieval object-wide distributions of measures are needed to accurately evaluate and compare local regions of shapes. Lien et al. proposed two point-wise concavity measures in the context of Approximate Convex Decompositions of polygons measuring the distance from a point to the polygon’s convex hull: an accurate Shortest Path-Concavity (SPC) measure and a Straight Line-Concavity (SLC) approximation of the same. While both are practicable on 2D shapes, the exponential costs of SPC in 3D makes it inhibitively expensive for a generalization to meshes. In this paper we propose an efficient and straight forward approximation of the Shortest Path-Concavity measure to 3D meshes. Our approximation is based on discretizing the space between mesh and convex hull, thereby reducing the continuous Shortest Path search to an efficiently solvable graph problem. Our approach works out-of-the-box on complex mesh topologies and requires no complicated handling of genus. Besides presenting a rigorous evaluation of our method on a variety of input meshes, we also define an SPC-based Shape Descriptor and show its superior retrieval and runtime performance compared with the recently presented results on the Convexity Distribution by Lian et al.
Polygon Mesh Repairing: An Application Perspective
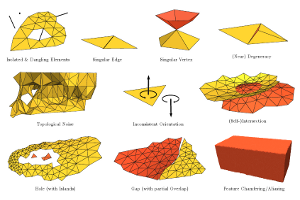
Nowadays, digital 3D models are in widespread and ubiquitous use, and each specific application dealing with 3D geometry has its own quality requirements that restrict the class of acceptable and supported models. This article analyzes typical defects that make a 3D model unsuitable for key application contexts, and surveys existing algorithms that process, repair, and improve its structure, geometry, and topology to make it appropriate to case-by-case requirements. The analysis is focused on polygon meshes, which constitute by far the most common 3D object representation. In particular, this article provides a structured overview of mesh repairing techniques from the point of view of the application context. Di fferent types of mesh defects are classified according to the upstream application that produced the mesh, whereas mesh quality requirements are grouped by representative sets of downstream applications where the mesh is to be used. The numerous mesh repair methods that have been proposed during the last two decades are analyzed and classified in terms of their capabilities, properties, and guarantees. Based on these classifications, guidelines can be derived to support the identification of repairing algorithms best-suited to bridge the compatibility gap between the quality provided by the upstream process and the quality required by the downstream applications in a given geometry processing scenario.
Practical Anisotropic Geodesy

The computation of intrinsic, geodesic distances and geodesic paths on surfaces is a fundamental low-level building block in countless Computer Graphics and Geometry Processing applications. This demand led to the development of numerous algorithms – some for the exact, others for the approximative computation, some focussing on speed, others providing strict guarantees. Most of these methods are designed for computing distances according to the standard Riemannian metric induced by the surface’s embedding in Euclidean space. Generalization to other, especially anisotropic, metrics – which more recently gained interest in several application areas – is not rarely hampered by fundamental problems. We explore and discuss possibilities for the generalization and extension of well-known methods to the anisotropic case, evaluate their relative performance in terms of accuracy and speed, and propose a novel algorithm, the Short-Term Vector Dijkstra. This algorithm is strikingly simple to implement and proves to provide practical accuracy at a higher speed than generalized previous methods.
Dual Loops Meshing: Quality Quad Layouts on Manifolds
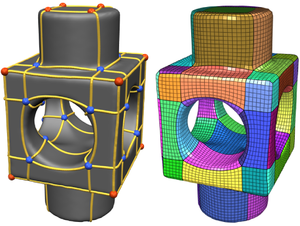
We present a theoretical framework and practical method for the automatic construction of simple, all-quadrilateral patch layouts on manifold surfaces. The resulting layouts are coarse, surface-embedded cell complexes well adapted to the geometric structure, hence they are ideally suited as domains and base complexes for surface parameterization, spline fitting, or subdivision surfaces and can be used to generate quad meshes with a high-level patch structure that are advantageous in many application scenarios. Our approach is based on the careful construction of the layout graph's combinatorial dual. In contrast to the primal this dual perspective provides direct control over the globally interdependent structural constraints inherent to quad layouts. The dual layout is built from curvature-guided, crossing loops on the surface. A novel method to construct these efficiently in a geometry- and structure-aware manner constitutes the core of our approach.
Rationalization of Triangle-Based Point-Folding Structures

In mechanical engineering and architecture, structural elements with low material consumption and high load-bearing capabilities are essential for light-weight and even self-supporting constructions. This paper deals with so called point-folding elements - non-planar, pyramidal panels, usually formed from thin metal sheets, which exploit the increased structural capabilities emerging from folds or creases. Given a triangulated free-form surface, a corresponding point-folding structure is a collection of pyramidal elements basing on the triangles. User-specified or material-induced geometric constraints often imply that each individual folding element has a different shape, leading to immense fabrication costs. We present a rationalization method for such structures which respects the prescribed aesthetic and production constraints and ?nds a minimal set of molds for the production process, leading to drastically reduced costs. For each base triangle we compute and parametrize the range of feasible folding elements that satisfy the given constraints within the allowed tolerances. Then we pose the rationalization task as a geometric intersection problem, which we solve so as to maximize the re-use of mold dies. Major challenges arise from the high precision requirements and the non-trivial parametrization of the search space. We evaluate our method on a number of practical examples where we achieve rationalization gains of more than 90%.
A Practical Guide to Polygon Mesh Repairing
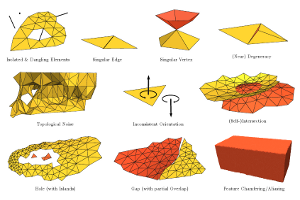
Digital 3D models are key components in many industrial and scientific sectors. In numerous domains polygon meshes have become a de facto standard for model representation. In practice meshes often have a number of defects and flaws that make them incompatible with quality requirements of specific applications. Hence, repairing such defects in order to achieve compatibility is a highly important task – in academic as well as industrial applications. In this tutorial we first systematically analyze typical application contexts together with their requirements and issues, as well as the various types of defects that typically play a role. Subsequently, we consider existing techniques to process, repair, and improve the structure, geometry, and topology of imperfect meshes, aiming at making them appropriate to case-by-case requirements. We present seminal works and key algorithms, discuss extensions and improvements, and analyze the respective advantages and disadvantages depending on the application context. Furthermore, we outline directions where further research is particularly important or promising.
Variational Tangent Plane Intersection for Planar Polygonal Meshing
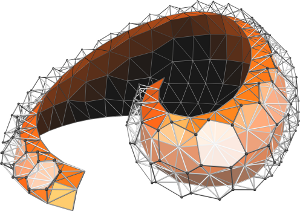
Several theoretical and practical geometry applications are based on polygon meshes with planar faces. The planar panelization of freeform surfaces is a prominent example from the field of architectural geometry. One approach to obtain a certain kind of such meshes is by intersection of suitably distributed tangent planes. Unfortunately, this simple tangent plane intersection (TPI) idea is limited to the generation of hex-dominant meshes: as vertices are in general defined by three intersecting planes, the resulting meshes are basically duals of triangle meshes.
The explicit computation of intersection points furthermore requires dedicated handling of special cases and degenerate constellations to achieve robustness on freeform surfaces. Another limitation is the small number of degrees of freedom for incorporating design parameters.
Using a variational re-formulation, we equip the concept of TPI with additional degrees of freedom and present a robust, unified approach for creating polygonal structures with planar faces that is readily able to integrate various objectives and constraints needed in different applications scenarios. We exemplarily demonstrate the abilities of our approach on three common problems in geometry processing.
Walking On Broken Mesh: Defect-Tolerant Geodesic Distances and Parameterizations

Efficient methods to compute intrinsic distances and geodesic paths have been presented for various types of surface representations, most importantly polygon meshes. These meshes are usually assumed to be well-structured and manifold. In practice, however, they often contain defects like holes, gaps, degeneracies, non-manifold configurations – or they might even be just a soup of polygons. The task of repairing these defects is computationally complex and in many cases exhibits various ambiguities demanding tedious manual efforts. We present a computational framework that enables the computation of meaningful approximate intrinsic distances and geodesic paths on raw meshes in a way which is tolerant to such defects. Holes and gaps are bridged up to a user-specified tolerance threshold such that distances can be computed plausibly even across multiple connected components of inconsistent meshes. Further, we show ways to locally parameterize a surface based on geodesic distance fields, easily facilitating the application of textures and decals on raw meshes. We do all this without explicitly repairing the input, thereby avoiding the costly additional efforts. In order to enable broad applicability we provide details on two implementation variants, one optimized for performance, the other optimized for memory efficiency. Using the presented framework many applications can readily be extended to deal with imperfect meshes. Since we abstract from the input applicability is not even limited to meshes, other representations can be handled as well.
Polygonal Boundary Evaluation of Minkowski Sums and Swept Volumes

We present a novel technique for the efficient boundary evaluation of sweep operations applied to objects in polygonal boundary representation. These sweep operations include Minkowski addition, offsetting, and sweeping along a discrete rigid motion trajectory. Many previous methods focus on the construction of a polygonal superset (containing self-intersections and spurious internal geometry) of the boundary of the volumes which are swept. Only few are able to determine a clean representation of the actual boundary, most of them in a discrete volumetric setting. We unify such superset constructions into a succinct common formulation and present a technique for the robust extraction of a polygonal mesh representing the outer boundary, i.e. it makes no general position assumptions and always yields a manifold, watertight mesh. It is exact for Minkowski sums and approximates swept volumes polygonally. By using plane-based geometry in conjunction with hierarchical arrangement computations we avoid the necessity of arbitrary precision arithmetics and extensive special case handling. By restricting operations to regions containing pieces of the boundary, we significantly enhance the performance of the algorithm.
A WebService employing this method is available.
Exact and Robust (Self-)Intersections for Polygonal Meshes

We present a new technique to implement operators that modify the topology of polygonal meshes at intersectionsand self-intersections. Depending on the modification strategy, this effectively results in operators for Boolean combinations or for the construction of outer hulls that are suited for mesh repair tasks and accurate meshbased front tracking of deformable materials that split and merge. By combining an adaptive octree with nested binary space partitions (BSP), we can guarantee exactness (= correctness) and robustness (= completeness) of the algorithm while still achieving higher performance and less memory consumption than previous approaches. The efficiency and scalability in terms of runtime and memory is obtained by an operation localization scheme. We restrict the essential computations to those cells in the adaptive octree where intersections actually occur. Within those critical cells, we convert the input geometry into a plane-based BSP-representation which allows us to perform all computations exactly even with fixed precision arithmetics. We carefully analyze the precision requirements of the involved geometric data and predicates in order to guarantee correctness and show how minimal input mesh quantization can be used to safely rely on computations with standard floating point numbers. We properly evaluate our method with respect to precision, robustness, and efficiency.
A WebService employing this method is available.
Hybrid Booleans
Talk at Eurographics 2011
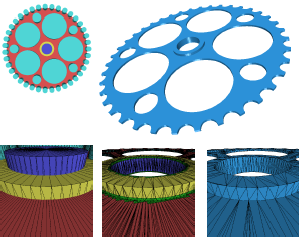
In this paper we present a novel method to compute Boolean operation polygonal meshes. Given a Boolean expression over an arbitrary number input meshes we reliably and efficiently compute an output mesh which faithfully preserves the existing sharp features and precisely reconstructs the new features appearing along the intersections of the input meshes. The term "hybrid" applies to our method in two ways: First, our algorithm operates on a hybrid data structure which stores the original input polygons (surface data) in an adaptively refined octree (volume data). By this we combine the robustness of volumetric techniques with the accuracy of surface-oriented techniques. Second, we generate a new triangulation only in a close vicinity around the intersections of the input meshes and thus preserve as much of the original mesh structure as possible (hybrid mesh). Since the actual processing of the Boolean operation is confined to a very small region around the intersections of the input meshes, we can achieve very high adaptive refinement resolutions and hence very high precision. We demonstrate our method on a number of challenging examples.
Ein Framework für Geometrieverarbeitung basierend auf hybriden Oberflächendarstellungen
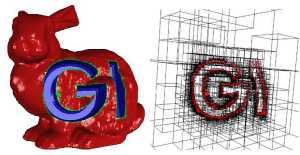
We present a framework that allows for the composition of custom-tailored data structures for hybrid representation of geometry and supports the development of associated geometry processing methods. Besides others, a novel hybrid approach for the evaluation of Boolean expressions on polygon meshes is elaborated in this context. By relying on the hybrid geometry information it is – in contrast to previous methods – able to perform such operations robustly as well as accurately.
A Framework for Geometry Processing based on Hybrid Surface Representations
We present a framework that allows for the composition of custom-tailored data structures for hybrid representation of geometry and supports the development of associated geometry processing methods. Besides others, a novel hybrid approach for the evaluation of Boolean expressions on polygon meshes is elaborated in this context.

